
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Программа курса лекций
1. Введение.
Цель курса. Метод Галилея.
Цель курса - активизировать теоретические основы физики, полученные в школе, научить студента их использовать для решения конкретных задач. Вводится система понятий - “язык” физики и устанавливается между ними взаимосвязь, повторяются и вводятся необходимые понятия элементарной математики и анализа, дается общий метод решения физических задач. Задачи, предлагаемые на занятиях, охватывают основные разделы школьной программы, с расширением и детализацией основных положений, соответствуют программе первого курса ФЕН НГУ.
Метод Галилея (МГ) – совокупность и последовательное выполнение действий, приводящих к решению конкретной задачи, появлению научного результата. Модельный подход при взгляде на окружающий мир и его изучении. От модели физической - к модели математической - системе уравнений, далее к решению, и далее через анализ и сопоставление с экспериментальными данными - к модели физической. Наука (физика) – совокупность предмета (природа) и метода изучения (МГ). Ньютон – первый ученик и первый ученый. Физическая модель. Математическая модель. Опыт. Принцип физический. Аксиоматическое построение Науки. Принципы, постулаты и законы как результат обобщения опыта. Принцип относительности. Принцип Гюйгенса. Принцип эквивалентности. Принцип наименьшего действия. Тождественные преобразования. Теория против эксперимента. Как решать задачи.
«Соображения симметрии». Требование инвариантности относительно сдвига и поворота в симметричном (однородном и изотропном) пространстве-времени.
Освоение МГ - основная причина быстрого развития науки и техники и естествознания в целом за последние 4 века.
Механика и наука физика «вообще» описывают, поясняют природу, мир до основных принципов, постулатов, законов. Почему мир таков, как он есть – вопрос к религии, к Создателю.
Механика - наука о движении тел в пространстве и во времени и возникающих взаимодействиях между ними.
Кинематика - часть механики, описывающая движение тел без выяснения причин.
Задача-свечка в ускоряющейся электричке.
Основные понятия.
Материальная точка (частица)- тело, малое в данном рассмотрении, по сравнению с масштабами рассматриваемого движения, другими телами.
Твердое тело – совокупность частиц с неизменными расстояниями между ними.
Пространство-Время – категории, обозначающие основные формы существования материи. В современной теории П и В – связаны.
Пространство – определяет порядок существования объектов.
Время – определяет порядок смены явлений.
По Ньютону П и В – абсолютны, не зависят друг от друга, находящихся в них тел и протекающих процессов. Пространство однородно (инвариантно по сдвигу) и изотропно (инвариантно по повороту). Время однородно.
Система отсчета – твердое тело, система координат, часы.
Числовая ось – прямая линия, на которой задано начало отсчета, единица масштаба и положительное направление.
Обозначение:  .
.
Координата точки на числовой оси – расстояние (со знаком) от начала отсчета до точки.
Обозначение:  .
.
Декартова система координат – совокупность трех (двух) взаимно перпендикулярных числовых осей  (осей координат) с общим началом отсчета.
(осей координат) с общим началом отсчета.
Обозначение:  .
.
Координата точки:  .
.
Координату точки получаем, опуская перпендикуляры из точки на оси координат.
Вектор – направленный отрезок. Имеет длину – модуль, и направление. Обозначение:  – черта сверху и/либо Ᾱ – жирный шрифт.
– черта сверху и/либо Ᾱ – жирный шрифт.
 ,
,
где  - проекции вектора
- проекции вектора  на оси координат,
на оси координат,  – орты (единичные вектора), направленные вдоль осей координат.
– орты (единичные вектора), направленные вдоль осей координат.
Модуль, длина, вектора:

Алгебра векторов – наука, которая занимается правилами преобразования векторов.
Сложение (вычитание) векторов:  ,
,
Разложение, умножение на число, равенство векторов.
Разложить любой вектор можно на произвольное количество векторов.
Умножить вектор на число – умножить на это число все его проекции.
Равными считаются вектора, которые при наложении совпадают.
Нулевой вектор.
Модуль такого равен нулю, направление не определено.
Пример – задача про четырех черепах (поворотная симметрия). Из одинаковости нач. условий и правил движения – одинаковые траектории.
Скалярное произведение векторов:  .
.

Правая (левая) системы координат (тройка векторов)  .
.
Если вектор  по кратчайшему углу вращать к вектору
по кратчайшему углу вращать к вектору  ,при этом связанный с ними правый буравчик ввинчивается вдоль вектора
,при этом связанный с ними правый буравчик ввинчивается вдоль вектора  , такая система (тройка векторов)
, такая система (тройка векторов)  называется правой (порядок имеет значение). Если вдоль вектора
называется правой (порядок имеет значение). Если вдоль вектора  ,то левой.
,то левой.
Или: если смотреть из конца вектора  , перпендикулярного плоскости, образованной векторами
, перпендикулярного плоскости, образованной векторами  , на эту плоскость, и при вращении вектора
, на эту плоскость, и при вращении вектора  квектору
квектору  по кратчайшему углу движение вектора
по кратчайшему углу движение вектора  происходит против часовой стрелки, то такая тройка векторов
происходит против часовой стрелки, то такая тройка векторов  наз. правой. Иначе – левой.
наз. правой. Иначе – левой.
Векторное произведение векторов:
 ;
; 
Вектора  образуютправую тройку векторов.
образуютправую тройку векторов.
Для  –правой тройки, состоящей из единичных векторов - орт, направленных вдоль осей координат, правило умножения:
–правой тройки, состоящей из единичных векторов - орт, направленных вдоль осей координат, правило умножения:
 .
.
Радиус-вектор
 .
.
Определяется тремя (одной, двумя) функциями. Р-в – вектор, идет из начала координат.
Полярная система координат на плоскости – содержит заданную точку плоскости О – полюс, семейство концентрических окружностей с центром в точке О и семейство лучей, исходящих из точки О. Один из лучей называют полярной осью.
Полярные координаты – расстояние до полюса (радиус  ) и угол
) и угол  между полярной осью и лучом, проходящим через полюс и рассматриваемую точку. Так же задается радиус-вектор точки на плоскости. Точка в полярных координатах обозначается так:
между полярной осью и лучом, проходящим через полюс и рассматриваемую точку. Так же задается радиус-вектор точки на плоскости. Точка в полярных координатах обозначается так:  .
.
Цилиндрическая и сферическая системы координат.
2. Функция
Функция – правило соотнесения значений независимой переменной (аргумента) и значений зависимой переменной (функции). Например,  – положение (координата) точки на числовой (координатной) оси
– положение (координата) точки на числовой (координатной) оси  , в зависимости от времени. Ф может быть векторной (напр., радиус-вектор).
, в зависимости от времени. Ф может быть векторной (напр., радиус-вектор).
Примеры функций:  - зависимость пройденного пути от времени при равноускоренном движении вдоль траектории;
- зависимость пройденного пути от времени при равноускоренном движении вдоль траектории;  - квадратичная зависимость.
- квадратичная зависимость.
Функция задается аналитически, графически, таблично.
Приращение функции – разница  между последующим и текущим значением функции.
между последующим и текущим значением функции.
 .
.
Временной интервал  – отрезок времени.
– отрезок времени.
 .
.
Задача-свечка во вращающейся комнате.
Производная функции – предел отношения приращения функции  к приращению аргумента
к приращению аргумента  , при стремлении приращения аргумента к нулю.
, при стремлении приращения аргумента к нулю.
 ,
,  ;
;
 ,
,  ,
, 
Геометрический смысл производной – тангенс угла наклона касательной к графику функции. Применение производной для исследования функции. Возрастание (убывание) функции, максимум (минимум) функции.
Функция возрастает, если производная положительна, убывает, если отрицательна. Если производная равна нулю, то функция принимает максимальное либо минимальное значение.
Пример – график скорости по графику пути (расстоянию) от точки наблюдения при движении по траектории.
Интегральная сумма – сумма произведений пронумерованных значений функции на соответствующие пронумерованные приращения аргумента. Значения функции выбираются в пределах соответствующего интервала изменения аргумента.
Определенный интеграл от функции - предельное значение интегральной суммы:

Здесь аргумент изменяется в пределах от  до
до  .
.
Первообразная функция.
Если существует такая дифференцируемая функция  , что
, что
 ,
,
то такая функция  является первообразной для функции
является первообразной для функции  .
.
Неопределенный интеграл:
 - множество всех первообразных.
- множество всех первообразных. 
Здесь  - первообразная функции
- первообразная функции  :
:  . Первообразная определена с точностью до константы:
. Первообразная определена с точностью до константы:
 ;
;

Формула Ньютона-Лейбница:
 ,
,
где  - первообразная функции
- первообразная функции  .
.
3. Движение по траектории.
Траектория частицы – кривая, по которой движется частица в пространстве/на плоскости.
Путь – длина участка траектории, пройденного за рассматриваемый отрезок времени:  .
.
Путь – сумма длин участков траектории:
 .
.
Путь – интеграл от скорости по времени в пределах от  до
до  :
:

Зеркальная симметрия. Задача об отражении в зеркале.
Перемещение – вектор, соединяющий начальную и конечную точки движения частицы. Может быть равно нулю – тело вернулось в исходную точку.
Пример – перемещение за день, от кровати до кровати.
Скорость средняя (модуль) – полный путь на полное время.
 .
.
Пример - пароход на реке.
Скорость мгновенная:
 .
.
Мгновенная скорость направлена вдоль вектора  - по касательной к траектории.
- по касательной к траектории.
На траектории движения мгновенная скорость:
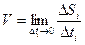 .
.
Ускорение:

Ускорение - вектор. Направление - вдоль вектора  . Угол
. Угол  между вектором скорости и вектором ускорения – произвольный, и лежит в пределах:
между вектором скорости и вектором ускорения – произвольный, и лежит в пределах:
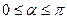 .
.
При  и
и  тело движется по прямой линии. При
тело движется по прямой линии. При  тело движется по окружности.
тело движется по окружности.
Пример – скорость и ускорение на параболе – траектории движения в однородном поле тяжести.
Угол – часть плоскости между двумя лучами, проведенными из одной точки.
Мера угла – отношение длины 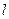 дуги окружности, отсекаемой лучами на окружности с центром в точке пересечения лучей, к радиусу
дуги окружности, отсекаемой лучами на окружности с центром в точке пересечения лучей, к радиусу 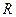 этой окружности:
этой окружности:
 .
.
Если  , угол
, угол  радиан.
радиан.
Скорость угловая:
 .
.
Из приведенных соотношений при постоянном радиусе следует:
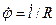 ,
,
или
 .
.
Здесь
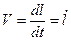
- линейная скорость движения точки по окружности.
 -псевдовектор,
-псевдовектор,  - псевдовектор.
- псевдовектор.
Пусть при движении по окружности (например, Земли вокруг Солнца) с угловой скоростью  ее радиус-вектор
ее радиус-вектор  переходит в радиус–вектор
переходит в радиус–вектор  .Вектора
.Вектора  образуют правую тройку векторов: если смотреть из конца вектора
образуют правую тройку векторов: если смотреть из конца вектора  , то при вращении вектора
, то при вращении вектора  к вектору
к вектору  движение вектора
движение вектора  происходит против часовой стрелки.
происходит против часовой стрелки.
Ускорение угловое:
 .
.
Уу – псевдовектор: вектора  образуют правую тройку векторов.
образуют правую тройку векторов.
Ускорение тангенцальное (касательное к траектории движения) – проекция полного вектора ускорения на мгновенную скорость частицы.
Ускорение центростремительное (нормальное к траектории движения) - проекция полного вектора ускорения на перпендикуляр к мгновенной скорости частицы.
Радиус кривизны траектории – радиус наибольшей окружности, касательной траектории в данной точке движения.
Задача – форма поверхности жидкости в стакане. Почему в покое поверхность жидкости в стакане параллельна поверхности Земли?
Скорость частицы в декартовых координатах.
Радиус-вектор частицы в момент времени t задается тремя (двумя, одной) функциями:  .
.  .
.
Производная от вектора.
Приращение радиус-вектора:
 .
.
Скорость частицы – производная радиус-вектора:
 .
. 
 .
.
В конечных разностях  .
.
В пределе, при  , средняя скорость переходит в мгновенную скорость, направление вектора перемещения и вектора мгновенной скорости совпадают. Мгновенная скорость направлена по касательной к траектории.
, средняя скорость переходит в мгновенную скорость, направление вектора перемещения и вектора мгновенной скорости совпадают. Мгновенная скорость направлена по касательной к траектории.
Модуль (величина) скорости:

 .
.
Ускорение частицы в декартовых координатах.

Равномерное движение.
В этом случае скорость не зависит от времени:
 ,
,
где  - постоянный вектор.
- постоянный вектор.
Радиус-вектор частицы:
 ,
,
где  – значение радиус-вектора частицы при t = 0.
– значение радиус-вектора частицы при t = 0.
 .
.
Направление вектора перемещения и вектора скорости совпадают. На координатной плоскости (в пространстве) частица двигается по прямой линии.
Задача- вектора скорости и ускорения на траектории движения.
4. Инвариантные и относительные величины.
Преобразования Галилея.
Инвариантными характеристиками движения называются такие характеристики, которые сохраняются при переходе из одной системы отсчета в другую.
Например, сохраняется временной интервал, длина отрезка, линейки, масса тела и т.д. При переходе из одной инерциальной системы отсчета в другую инерциальную систему сохраняется величина ускорения тела.
Относительными величинами называются такие величины, которые меняются при переходе из одной системы отсчета в другую. В кинематике это координаты тела, перемещение, скорость. Если хотя бы одна из систем отсчета является неинерциальной, то при переходе может меняться и ускорение тела.
Преобразования Галилея.

Пусть в лабораторной системе отсчета  с началом координат в точке
с началом координат в точке  движется частица, при этом ее текущий радиус-вектор
движется частица, при этом ее текущий радиус-вектор  .
.
Соответственно, скорость частицы в этой системе отсчета  ,
,
ускорение  .
.
Пусть относительно лабораторной системы  движется система отсчета
движется система отсчета  с началом в точке
с началом в точке  . При этом в системе
. При этом в системе  радиус-вектор точки
радиус-вектор точки  равен
равен  , скорость движущейся системы
, скорость движущейся системы  относительно лабораторной (относительная скорость)
относительно лабораторной (относительная скорость)  .
.
В движущейся системе отсчета:
радиус-вектор частицы  ,
,
скорость  ,
,
ускорение  .
.
В ньютоновской механике предполагается, что время во всех системах отсчетах течет одинаково, время абсолютно:  .
.
Тогда справедливы соотношения:
 ; или
; или 
Если относительное ускорение движущейся системы отсчета равно нулю, т.е.  , то величина ускорения частицы сохраняется:
, то величина ускорения частицы сохраняется:  . Например, ускорение инвариантно относительно перехода из одной инерциальной системы отсчета в другую инерциальную систему. Это следует из того, что в этом случае
. Например, ускорение инвариантно относительно перехода из одной инерциальной системы отсчета в другую инерциальную систему. Это следует из того, что в этом случае  .
.
Преобразования Галилея связывают координаты и время в одной инерциальной системе отсчета с координатами и временем в другой инерциальной системе отсчета:

5. Динамика. Законы Ньютона.
Основные понятия.
Уравнения движения - соотношения, связывающие ускорение частицы с координатами и скоростями.
Законы сохранения - соотношения, определяющие инвариантные (неизменные) величины при движении системы.
Масса – характеристика внутреннего состояния частицы, определяющая ее энергию (E=mc2), «интенсивность» гравитационного взаимодействия с другими частицами (F=GmM/r2), «интенсивность» сопротивления изменению скорости (F=ma) - мера инерции.
Инерция – способность тела сохранять состояние покоя или прямолинейного и равномерного движения. «Тело двигается по инерции…».
Импульс частицы  , импульс системы частиц
, импульс системы частиц  .
.
Импульс вектор, как и скорость.
Сила – мера взаимодействия тел.
Принцип суперпозиции – суммарное действие независимых причин равно сумме действий этих причин.
Замкнутая система – система, не подверженная действию внешних сил.
Сила трения покоя и скольжения - силы, возникающие при скольжении тел. Приложены в точке взаимодействия тел и лежат в касательной плоскости. Направлены против вектора возможного смещения или скорости.
Тяготение - свойство масс взаимодействовать на расстоянии. Одно из четырех фундаментальных взаимодействий (сильное, слабое, электромагнитное, гравитационное).
Вес - сила действия тела на опору.
Сила реакции – сила, возникающая при контактном взаимодействии тел. Приложена к телу в точке взаимодействия тел и направлена по нормали к касательной плоскости.
Законы Ньютона.
Первый закон Ньютона-закон инерции:
Существуют системы отсчета, в которых тела, свободные от внешних воздействий, движутся прямолинейно и равномерно. Такие системы отсчета называют инерциальными.
Или: если на тело не действует сила, тело сохраняет состояние покоя или прямолинейного и равномерного движения.
Принцип относительности Галилея:
Механические явления (законы) одинаковы во всех инерциальных системах отсчета. Инерциальные системы отсчета эквивалентны. Время абсолютно. Для полного совпадения необходима одинаковость начальных условий.
Второй закон Ньютона:
 .
.
Такое уравнение называется также уравнением движения тела. Для системы тел:
 .
.
Движение по параболе в однородном поле тяжести.
Поскольку  , уравнение движения и, соответственно, собственно движение тела распадается на три явно не зависимых движения по трем координатам:
, уравнение движения и, соответственно, собственно движение тела распадается на три явно не зависимых движения по трем координатам:
 ;
;  ;
;  .
.
Поле тяжести направим по оси Y , т.е. оси координат расположим так, что  . Тогда
. Тогда  ,
,  и соответствующие уравнения движения имеют вид:
и соответствующие уравнения движения имеют вид:
 ; (1)
; (1)
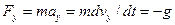 (2)
(2)
 (3)
(3)
Пусть из пушки выстреливают снаряд со скоростью  , т.е.
, т.е.
 ,
,  ,
,  .
.
Расположим пушку в начале координат. Еще одно условие на расположение пушки: «без ограничения общности» можно положить  . Тогда решение системы (1), (2), (3) при оговоренных начальных условиях будет иметь вид:
. Тогда решение системы (1), (2), (3) при оговоренных начальных условиях будет иметь вид:
 ;
;  ;
;  .
.
Соответственно
 ;
;  ;
;  .
.
Траектория движения снаряда в однородном поле лежит в одной плоскости  , т.е. в плоскости
, т.е. в плоскости  .
.
Из последних уравнений находим явный вид зависимости координаты  от координаты
от координаты  при полете снаряда по траектории - уравнение траектории:
при полете снаряда по траектории - уравнение траектории:
 .
.
Снаряд двигается по параболе.
Максимальная высота полета  , при этом
, при этом  .
.
В точке падения снаряда  .
.
Время подъема до верхней точки  . Время полета равно времени спуска. Траектория симметрична относительно верхней точки полета.
. Время полета равно времени спуска. Траектория симметрична относительно верхней точки полета.
Вектора скорости и ускорения на траектории движения.
Третий закон Ньютона.
Для двух взаимодействующих тел a,b:
 .
.
 - cила действия на тело a со стороны тела b численно равна и противоположна
- cила действия на тело a со стороны тела b численно равна и противоположна  – силе, действующей на тело b со стороны тела a. По третьему ЗН при взаимодействии тел силы всегда возникают парами; силы направлены в противоположные стороны и приложены к разным телам. Для замкнутой (изолированной) системы взаимодействующих тел
– силе, действующей на тело b со стороны тела a. По третьему ЗН при взаимодействии тел силы всегда возникают парами; силы направлены в противоположные стороны и приложены к разным телам. Для замкнутой (изолированной) системы взаимодействующих тел  (сумма внутренних сил равна нулю).
(сумма внутренних сил равна нулю).
Основные задачи. 1.Движение тела под действием силы. 2.Движение связанных тел. Натяжение невесомой нерастяжимой веревки. 3.Натяжение веревки, имеющей погонную плотность. 4.Блоки 5.Тело на наклонной плоскости. 6.Дорога движет автомобиль.
Закон всемирного тяготения (Ньютон, 1665 г.).
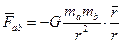
Сила действия на частицу массы  со стороны частицы массы
со стороны частицы массы  направлена по прямой линии, их соединяющей. Здесь
направлена по прямой линии, их соединяющей. Здесь  – радиус вектор, проведенный из точки расположения частицы
– радиус вектор, проведенный из точки расположения частицы  к точке расположения частицы
к точке расположения частицы  ,
,  - соответственно расстояние между частицами. Тела притягиваются друг к другу: вектор силы гравитационного взаимодействия тел (вектор силы тяжести) направлен против направления вектора
- соответственно расстояние между частицами. Тела притягиваются друг к другу: вектор силы гравитационного взаимодействия тел (вектор силы тяжести) направлен против направления вектора  .
.
 - универсальная гравитационная постоянная.
- универсальная гравитационная постоянная.
Поле тяжести.
Напряженность гравитационного поля, поле тяжести, создаваемое телом массы  :
:

Вблизи Земли поле тяжести близко к однородному полю, при этом ускорение свободного падения  .
.
Задача о поле внутри однородного шара, сферы. Степень однородности гравитационного поля Земли.
6. Работа. Энергия. Закон сохранения механической энергии.
Механическая работа.
Элемент работы 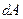 силы
силы  над телом – скалярное произведение силы, действующей на тело, на перемещение
над телом – скалярное произведение силы, действующей на тело, на перемещение  :
:

В конечных разностях

В общем случае для произвольного вектора  можно записать:
можно записать:

Поэтому

где  – кинетическая энергия тела.
– кинетическая энергия тела.
Силу, действующую на тело, можно разложить на две составляющие – проекции: параллельную и перпендикулярную перемещению  . Точно также можно разложить и мгновенную скорость частицы. Работу совершает только первая часть силы. За счет действия силы меняется параллельная проекция скорости; перпендикулярная проекция скорости при этом сохраняется. При изменении скорости частицы меняется ее кинетическая энергия.
. Точно также можно разложить и мгновенную скорость частицы. Работу совершает только первая часть силы. За счет действия силы меняется параллельная проекция скорости; перпендикулярная проекция скорости при этом сохраняется. При изменении скорости частицы меняется ее кинетическая энергия.
Т.е. справедлива теорема о кинетической энергии: работа силы равна изменению кинетической энергии тела.
Работа консервативной силы на криволинейной траектории.
Консервативной называется сила (соответственно, консервативным называется порождающее ее силовое поле), работа  которой при перемещении тела из точки А, с радиусом-вектором
которой при перемещении тела из точки А, с радиусом-вектором  в точку Б, с радиусом-вектором
в точку Б, с радиусом-вектором  , не зависит от формы траектории. Работу
, не зависит от формы траектории. Работу  можно представить в виде приращения некоторой функции
можно представить в виде приращения некоторой функции 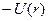 :
:
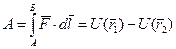 .
.
Функция  называется потенциальной энергией тела в точке
называется потенциальной энергией тела в точке
 .
.
Работа консервативной силы по замкнутому контуру равна нулю:

Справедливо и обратное утверждение: если работа силы по замкнутому контуру равна нулю, то такая сила (поле) является консервативной, т.е. работа силы не зависит от формы траектории.
Однородным называется поле, сила действия которого не зависит от координат.
Близким к однородному полю является поле тяжести вблизи Земли. Вблизи Земли на тело массы  действует направленная к Земле сила
действует направленная к Земле сила
 .
.
Потенциальная энергия в однородном поле тяжести.
Поле тяжести  не зависит от координат, консервативно.
не зависит от координат, консервативно.
Элемент работы в декартовых координатах

При перемещении их точи А в точку Б совершается работа

Выберем систему координат  с направлением оси
с направлением оси  вдоль поля тяжести:
вдоль поля тяжести:  ,
,  . Тогда при перемещении тела из точки
. Тогда при перемещении тела из точки  в точку
в точку  работа силы тяжести
работа силы тяжести
 .
.
Для однородного поля тяжести можно ввести функцию
 ,
,
Функцию  называют потенциальной энергией тела в поле тяжести.
называют потенциальной энергией тела в поле тяжести.
Работа силы тяжести равна убыли потенциальной энергии тела:
 .
.
«Без ограничения общности» можно положить  , т.е.
, т.е.
 .
.
Однородное поле тяжести является консервативным полем, поскольку

Закон сохранения механической энергии тела.
Пусть тело находится в некотором силовом поле, например, поле тяжести, и приводится в движение этим полем (сила  ) и другой силой, например, силой тяги ракетного двигателя (сила
) и другой силой, например, силой тяги ракетного двигателя (сила  ).Тогдасуммарная сила
).Тогдасуммарная сила
 и
и 
Или

Обозначим
 , где
, где
 - потенциальная энергия тела.
- потенциальная энергия тела.
В этих обозначениях работа силы тяжести  над телом приводит к убыли его потенциальной энергии
над телом приводит к убыли его потенциальной энергии  .
.
Окончательно:
 .
.
Работа силы равна изменению полной - потенциальной и кинетической энергии тела - теорема о полной механической энергии тела.
При  ,
,
 , т.е.
, т.е.
 .
.
Т.о., выполняется закон сохранения механической энергии: если тело находится в поле тяжести, а другая сила (кроме силы тяжести), действующая на тело, равна нулю, полная механическая энергия тела сохраняется.
7. Закон сохранения импульса.
Импульс силы.
Импульсом силы называют величину  - произведение силы, действующей на тело, на время ее действия.
- произведение силы, действующей на тело, на время ее действия.
Второй закон Ньютона в конечных разностях
 . Или
. Или

Импульс действующей на тело силы, равен изменению импульса тела.
Если  , то
, то  и
и  .
.
Выполняется закон сохранения импульса:
Если на тело не действует сила, его импульс сохраняется.
Рассмотрим систему взаимодействующих тел (силы взаимодействия  ,
,  ). Кроме того, пусть на эти тела действуют внешние силы (
). Кроме того, пусть на эти тела действуют внешние силы (  на тело
на тело  ,
,  на тело
на тело  ). Тогда
). Тогда
 ,
,  .
.
Складывая левые и правые части системы уравнений получим:
 , или
, или
 .
.
Поскольку суммирование идет по одним и тем же частицам,
 .
.
Сумма изменения импульсов частиц равна изменению импульса системы:
 .
.
По третьему ЗН
 .
.
В результате выполняется соотношение:
 ,
,
суммарный импульс силы внешних по отношению к системе сил равен изменению импульса системы.
Если сумма внешних сил равна нулю, т.е. если  , то
, то  , и, соответственно,
, и, соответственно,
 .
.
Для замкнутой системы справедлив закон сохранения импульса:
импульс замкнутой системы тел сохраняется.
Система центра инерции.
Рассмотрим систему движущихся частиц с массами  , координатами
, координатами  , и скоростями
, и скоростями  . В лабораторной системе отсчета полный импульс частиц
. В лабораторной системе отсчета полный импульс частиц  . В системе, начало отсчета которой имеет радиус вектор
. В системе, начало отсчета которой имеет радиус вектор  , движущейся относительно лабораторной с некоторой скоростью
, движущейся относительно лабораторной с некоторой скоростью  , полный импульс частиц
, полный импульс частиц
 .
.
Соответственно,
 .
.
Можно выбрать систему отсчета, в которой полный импульс частиц равен нулю,  . Относительно лабораторной системы отсчета ее скорость определяется из соотношения:
. Относительно лабораторной системы отсчета ее скорость определяется из соотношения:
 .
.
Количество таких систем отсчета бесконечно.
Одна из движущихся со скоростью  систем отсчета, радиус – вектор начала отсчета которой определяется из соотношения
систем отсчета, радиус – вектор начала отсчета которой определяется из соотношения
 ,
,
называется системой центра инерции тел. Скорость движения системы ЦИ в лабораторной системе определяется как полная производная от выражения для радиуса – вектора ее начала:

В системе ЦИ полный импульс системы тел равен нулю, 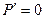 .
.
Подставляя в выражение для радиуса-вектора  соотношение
соотношение  , получаем, что в системе центра инерции выполняется соотношение:
, получаем, что в системе центра инерции выполняется соотношение:

Точку, относительно которой выполняется приведенное соотношение, еще называют центром масс.
Например, центр масс двух частиц с массами  , находящихся друг от друга на расстоянии X, расположен на линии, их соединяющей. Координата первой частицы относительно центра масс
, находящихся друг от друга на расстоянии X, расположен на линии, их соединяющей. Координата первой частицы относительно центра масс  , второй частицы
, второй частицы  . Ось X направлена от второй частицы к первой.
. Ось X направлена от второй частицы к первой.
Может оказаться, что центр масс находится вне тела. Так, центр масс колеса находится на его оси.
Столкновение частиц.
Упругим называется столкновение частиц, если оно не сопровождается изменением их внутреннего состояния. При этом сохраняется полный импульс частиц и суммарная кинетическая энергия.
Рассмотрим столкновение двух частиц. В системе ЦИ такой процесс выглядит наиболее просто. Полный импульс равен нулю, поэтому до и после столкновения импульсы частиц равны по величине и противоположны по направлению. По закону сохранения энергии остаются неизменными и абсолютные значения импульсов. Массы частиц при ударе также не меняются. Поэтому при упругом столкновении двух частиц происходит поворот их скоростей, остающихся неизменными и противонаправленными.
В лабораторной системе отсчета упругое столкновение двух частиц также определяется законами сохранения.
Пусть одна из частиц до удара покоилась. Для импульса и энергии частиц можно записать.
 .
.

Возведя первое уравнение в квадрат, получим:

Для частиц одинаковой массы из приведенных соотношений получаем

Скалярное произведение векторов скоростей равно нулю, поэтому в лабораторной системе отсчета возможны два варианта. В первом случае после столкновения обе скорости отличны от нуля и частицы разлетаются под прямым углом. Во втором случае первая частица останавливается,  , а вторая начинает двигаться со скоростью первой до удара,
, а вторая начинает двигаться со скоростью первой до удара,  . Это соответствует т.н. центральному удару.
. Это соответствует т.н. центральному удару.
Центральным называется столкновение (удар), при котором импульсы частиц до и после столкновения лежат на одной прямой. В системе ЦИ при упругом центральном ударе двух частиц их скорости меняют знак, оставаясь на той же прямой и неизменными по величине.
Неупругим называется удар, при котором часть энергии переходит во внутреннюю энергию тел.
Абсолютно неупругий удар характеризуется тем, что при столкновении двух тел образуется одно тело с общей массой. В системе ЦИ скорость этого тела равна нулю, вся кинетическая энергия тел в результате столкновения переходит во внутреннюю энергию образовавшегося тела.
8. Закон Гука. Гармонические колебания.
Силы упругости – силы, возникающие при удлинении пружины, стержня. Сила упругости пропорциональна удлинению и направлена в сторону, противоположную направлению удлинения тела (закон Гука – 1676 г.):

 – коэффициент жесткости,
– коэффициент жесткости,  – удлинение пружины, стержня.
– удлинение пружины, стержня.
Для стержня
 ,
,
 - модуль Юнга, размерность-давление,
- модуль Юнга, размерность-давление,
 - поперечное сечение стержня,
- поперечное сечение стержня,
 - длина стержня.
- длина стержня.
Для стали  .
.
Рассмотрим движение тела массы  , прикрепленного к пружине с жесткостью
, прикрепленного к пружине с жесткостью  . На тело действует сила упругости пружины
. На тело действует сила упругости пружины  . По второму закону Ньютона
. По второму закону Ньютона
 .
.
Соответствующее уравнение движения тела, прикрепленного к пружине, будет иметь вид:
 ,
,
или

где введено обозначение
 .
.
Данное дифференциальное уравнение второго порядка описывает гармонические колебания тела около положения равновесия.
Решение уравнения имеет вид:
 , где
, где
 - амплитуда колебаний,
- амплитуда колебаний,
 - фаза колебаний, и
- фаза колебаний, и
 - начальная фаза,
- начальная фаза,
 - циклическая (круговая) частота.
- циклическая (круговая) частота.
Периодом колебаний называют величину

Величину

называют частотой колебаний. Фактически  - это количество колебаний в секунду.
- это количество колебаний в секунду.
Для простоты далее положим  .
.
Дифференцируя координату по времени, получим скорость тела  :
:
 ,
,
и ускорение  :
:
 .
.
Величины
 и
и 
- соответственно максимальные скорость и ускорение тела в процессе колебаний.
Из приведенных уравнений видно, что скорость колеблющегося тела «опережает» по фазе координату на угол 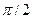 , ускорение «опережает» по фазе скорость на угол
, ускорение «опережает» по фазе скорость на угол 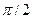 , координата тела и ускорение находятся в противофазе.
, координата тела и ускорение находятся в противофазе.
9. Движение по окружности. Твердое тело.
Нормальное ускорение – проекция полного ускорения на нормаль к траектории движения тела.
Тангенциальное или касательное ускорение тела – проекция полного ускорения на направление касательной к траектории движения тела.
Центростремительное ускорение – ускорение, возникающее при движении тела по окружности. Направлено к центру окружности, по которой движется тело.
Угол – часть плоскости между двумя лучами, проведенными из одной точки.
Мера угла – отношение длины 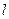 дуги окружности, отсекаемой лучами на окружности с центром в точке пересечения лучей, к радиусу
дуги окружности, отсекаемой лучами на окружности с центром в точке пересечения лучей, к радиусу 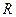 этой окружности:
этой окружности:
 .
.
Если  , угол
, угол  радиан.
радиан.
Из приведенного соотношения при постоянном радиусе следует:
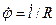 ,
,
или
 .
.
Здесь
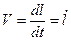
- линейная скорость движения точки по окружности;

- угловая скорость.
При движении тела по окружности с постоянной по модулю скоростью вектор скорости поворачивается, т.е. скорость, вообще говоря, переменна. Вектор скорости  перпендикулярен радиус-вектору тела
перпендикулярен радиус-вектору тела  . При повороте радиус-вектора
. При повороте радиус-вектора  на некоторый угол
на некоторый угол  на такой же угол поворачивается вектор скорости
на такой же угол поворачивается вектор скорости  . В соответствии с этим при малых углах поворота
. В соответствии с этим при малых углах поворота

и аналогично
 .
.
Вектор  при движении окружности направлен перпендикулярно вектору
при движении окружности направлен перпендикулярно вектору  , вектор
, вектор  направлен вдоль вектора
направлен вдоль вектора  и перпендикулярен вектору
и перпендикулярен вектору  , а вектор
, а вектор  перпендикулярен скорости и направлен к центру вращения. Разделив правую и левую часть соотношений на время
перпендикулярен скорости и направлен к центру вращения. Разделив правую и левую часть соотношений на время  , в течение которого происходит поворот на угол
, в течение которого происходит поворот на угол  , для скорости
, для скорости
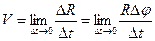
и центростремительного ускорения

получим:


Эквивалентные выражения:


При движении по окружности с постоянной по модулю скоростью тело двигается с постоянным по модулю ускорением, направленным к центру вращения. Соответственно, движение по окружности тела массы  осуществляется под действием силы:
осуществляется под действием силы:

Эта сила направлена к центру вращения, потому ее называют центростремительной силой. Роль центростремительной силы может выполнять сила трения при движении автомобиля на повороте дороги, сила натяжения веревки при вращении привязанного тела, например камня, сила тяжести.
Спутник на орбите.
Примером движения тела под действием центростремительной силы является движение космического корабля по круговой орбите вокруг Земли. В этом случае роль центростремительной силы выполняет сила притяжения корабля к Земле. По второму закону Ньютона:

Вблизи Земли

В соответствии с этим первая космическая скорость
 .
.
Подставляя значения  , радиус Земли
, радиус Земли  , получим
, получим
Дата добавления: 2014-10-31; просмотров: 360; Мы поможем в написании вашей работы!; Нарушение авторских прав