Расчет цепей переменного тока.

В любой цепи переменного тока различают элементы трех типов: R,L,C.

R- активное сопротивление – элемент, в котором происходит необратимое преобразование электрической энергии в тепловую;

L- индуктивность – элемент, в котором происходят обратимое преобразование электрической энергии в магнитную;

C- ёмкость – элемент, способный накапливать, удерживать, а затем возвращать электрическую энергию.

Цепи, в которых один из трёх параметров значительно преобладает над двумя другими настолько, что ими можно пренебречь и считать, что в цепи всего один элемент, такие цепи называют идеальными.

3.4.1 Идеальная цепь с активным сопротивлением R(L=0, C=0)

Для цепей переменного тока в силе законы Ома и Кирхгофа.

Пусть U приложенное к зажимам цепи меняется по закону

u = U_m sin wt

Ток в любой момент времени можно найти по закону Ома i=

Активное сопротивление R не вызывает сдвиг по фазе между U и I. Но R, U и I всегда совпадают по фазе.

- закон Ома для амплитудных значений

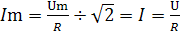– закон Ома для действующих значений

Только в этой цепи закон Ома записывается во всех формах (для мгновенных, амплитудных и действующих значений U и I).

p= U_m sin wt*I_m sin wt= - cos 2wt.

u= U_m sin wt

i= I_m sin wt

p= - cos 2wt

Из градусов видно, что в течение всего периода Т p≥0, это значит, что направление потока энергии всегда одинаково и в цепи она преобразуется в другой вид. Характеристики этого процесса вводят понятие активной мощности P под которой понимают среднее значение мгновенной мощности взятое за период.

P= =UI (т.к. 2=√2*√2)=I²R, Вт

Расчетные формулы в данной цепи такие же как и в обычной.

3.4.2 Идеальная цепь с ёмкостью. C(L=0, R=0)

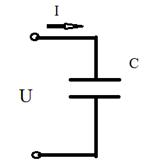
Т.к. ёмкость элемент способный накапливать, а затем отдавать электрическую энергию зависит от напряжения, то для вывода закономерностей задается законом изменения напряжения.

u= U_m sin wt

i=

i= (ток опережает напряжение по фазе).

Ёмкость (С) вызывает сдвиг по фазе между напряжением и током. На ёмкости ток опережает по фазе напряжение на 90°.

I_m=cU_mω=

- закон Ома для амплитуд, (:√2) I_m= – закон Ома для действующих значений.

Для мгновенных значений закон Ома не существует.

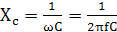Реактивное сопротивление ёмкости обратно пропорционально частоте протекающего тока, чем выше частота, тем меньшее сопротивление оказывает конденсатор переменному току. Если частота равна 0, это значит течет постоянный ток для него конденсатор имеет бесконечно большое сопротивление (постоянный ток через конденсатор не протекает).

i=

P= =sin 2wt

u= U_m sin wt

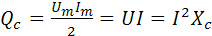ВАР

Из графиков видно, что в первую четверть периода и напряжение и ток положительные, это значит, энергия поступает из генератора в цепь, происходит зарядка конденсатора. Во вторую четверть периода U(+), a I(-), поэтому P=(+)*(-)=(-)→ конденсатор разряжается на генератор.

3.4.3 Расчет реальных цепей при последовательном соединении элементов.

Данную схему можно рассматривать: а) как последовательное соединение двух альных элементов, тогда U, U_A, U_L существуют реально, их можно измерить; б) как схему замещения реальной катушки индуктивности, тогда U_A и U_L существуют теоретически, измерить их нельзя.

Расчет цепи произведен с помощью построения векторной диаграммы и формул выведенных из треугольников U, R,P.

Согласно второму закону Кирхгофа для мгновенных значений U=U_A+U_L

При построении векторной диаграммы для удобства вывода формул начальную фазу тока берем равную нулю.

0<φ<90

В такой цепи напряжение опережает по фазе ток на угол φ<90°.

Построим треугольник напряжений, для этого вектора напряжений сложим по правилу треугольника.

U=