I. Теоретические сведения. Электротехника и ТОЭ в примерах и задачах: Практическое пособие

Электротехника и ТОЭ в примерах и задачах: Практическое пособие. – СПб.: Издательство «Корона. Век», 2012.-336 с., ил.

http://www.electrik.org/lesson/Golubev/default.htm

I. Теоретические сведения.

Определения вектора, суммы, разности двух векторов, умножения вектора на число, скалярного произведения векторов вводятся в пространстве так же, как и на плоскости.

Векторы называются компланарными, если они лежат в одной плоскости или существует плоскость, которой они параллельны.

Сумму трех некомпланарных векторов можно получить по правилу параллелепипеда. Отложим от некоторой точки О пространства

Совокупность трех некомпланарных векторов, взятых в определенном порядке, называется базисом векторного пространства. Число векторов базиса определяет размерность векторного пространства.

В = 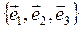– аффинный базис В = – ортонормированный базис

Dim V = 3 Dim V = 3

Базис называется ортонормированным, если выполняются следующие условия: 1) , ,

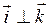2)

Коэффициенты разложения вектора по векторам базиса называются координатами вектора относительно данного базиса.

Т.е., если то относительно базиса В = .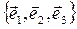

Для того чтобы векторы были компланарными, необходимо и достаточно, чтобы определитель, составленный из координат этих векторов был равен 0. Т.е. 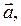- компланарны 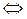= 0, где , , .

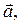
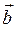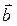
В дальнейшем будем рассматривать только ортонормированный базис. Пусть заданы координатами, то есть , . Тогда операции над векторами в координатах выражаются следующим образом:

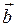
λ

=

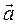
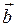(1)

cos

sin

Есл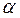и , и 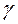– углы, которые составляет с базисными векторами, т.е. = , = , = , то cos , cos , cos называются направляющими косинусами вектора .

Пусть 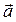имеет координаты a₁, a₂, a₃, тогда

a₁ = 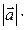cos

a₂ = 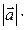cos (2)

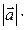a₃ = cos

Формулы (2) выражают геометрический смысл координат 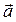относительно ортонормированного базиса.

Из (1) и (2) следует, что

cos² + cos² + cos² = 1

Последнее равенство позволяет определить один из углов , , , если известны два других.

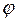Проекцией на ось u называется число, равное произведению длины вектора на косинус угла наклона вектора к оси u.

пр_u = 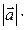cos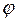

Используя операцию скалярного произведения векторов, проекцию произвольного вектора на какую-нибудь ось u можно определить формулой

пр_u ,

где – единичный вектор, направленный по оси u.

Если даны углы 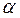, , , которые ось u составляет с координатными осями, то и проекция вектора на ось u вычисляется по формуле:

пр_u =