I. Теоретические сведения. Аффинной системой координат (или аффинным репером) в пространстве называется совокупность точки О пространства и упорядоченной тройки линейно-независимых

Аффинной системой координат (или аффинным репером) в пространстве называется совокупность точки О пространства и упорядоченной тройки линейно-независимых векторов .

R = .

		Точка О называется началом системы координат. Координатные оси Ox, Oy, Oz называются соответственно осями абсцисс, ординат и аппликат, а плоскости Oxy, Oyz, Oxz – координатными плоскостями. Векторы называются базисными векторами.

Аффинная система координат называется прямоугольной декартовой системой координат, если ее базисные векторы единичны и попарно ортогональны.

В дальнейшем мы будем пользоваться только правой системой координат.

Под координатами точки М пространства мы будем понимать координаты ее радиус-вектора .

М(x, y, z)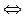

Точка М(x, y, z) принадлежит плоскости Oxy тогда и только тогда, когда z = 0.

Аналогично, М(x, y, z) Oyz x = 0,

М(x, y, z) Oxz 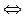y = 0.

Точка М(x, y, z) лежит на оси Ox тогда и только тогда, когда y = 0 и z = 0.

Аналогично, М(x, y, z) Oy 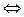x = 0, z = 0

М (x, y, z) Oz x = 0, y = 0.

Координаты вектора в пространстве равны разности соответствующих координат конца В и начала А вектора.

, где A(x₁, y₁, z₁), B(x₂, y₂, z₂).

Говорят, что точка М делит отрезок М₁М₂ в отношении , если .

Пусть относительно некоторой аффинной системы координат М₁(x₁, y₁, z₁), М₂(x₂, y₂, z₂), тогда координаты точки М, делящей отрезок М₁М₂ в отношении ( ) вычисляются по формулам:

, , .

Если М – середина отрезка М₁М₂, то и тогда

, , .

Расстояние между двумя точками в пространстве A(x₁;y₁;z₁), B(x₂;y₂;z₂), заданными своими координатами в прямоугольной декартовой системе координат вычисляется по формуле:

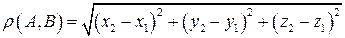
Формулы преобразования координат при переходе от старой аффинной системы координат R = 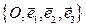к новой R' = имеют вид:

где О'(x₀, y₀,z₀)_R,

det C = det (C^T) 0, где 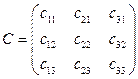– матрица перехода от старого базиса к новому.

Если R и R' – прямоугольные декартовы системы координат, то матрицы С и С^Т являются ортогональными. (det (C) = det (C^T) = ).