
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
V. Задачи для самостоятельной работы.
1. Дано изображение ПДСК. Изобразите точки А(2; 3; 1), В(–1; 4; 0), С(4; 2; –5), D(–3; –1; –5).
2. Доказать, что четырехугольник, вершины которого находятся в точках А(7; 2; 4), В(4; –4; 2), С(6; –7; 8), D(9; –1; 10), является квадратом.
3. Даны координаты трех вершин параллелепипеда ABCDA¢B¢C¢D¢, а также точки О пересечения его диагоналей: А(2; 1; –1), В(3; 3; 4), С(–1; –1; 0), О(2; 2; 3). Найдите координаты остальных вершин.
4. Даны координаты двух вершин равностороннего треугольника 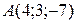 и
и 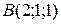 . Найдите его площадь.
. Найдите его площадь.
5. Даны вершины треугольника А(2; –1; 4), В(3; 2; –6), С(–5; 0; 2). Вычислить длину его медианы, проведенной из вершины А.
6. Даны четыре точки А(0; 1; –1), В(1; 0; 1), С(–1; 1; 0), D(1; –1; 1). Найти точку одинаково удаленную от данных точек.
7. Даны координаты двух вершин треугольника АВС: А(–4, –1, 2), В(3, 5,
–6). Найдите координаты третьей вершины, если известно, что середина стороны АС лежит на оси Oy, а середина стороны ВС – на плоскости xOz.
8. На прямой, проходящей через точки А(1; 0; 4) и В(3; –1; 2) найти точку С такую, чтобы АС=3АВ и точка В лежала между точками А и С.
9. На прямой l взяты последовательно точки 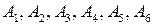 , так что
, так что  . Зная координаты точек
. Зная координаты точек  и
и 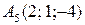 , определить отношения, в которых точки
, определить отношения, в которых точки 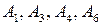 делят отрезок
делят отрезок 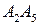 , также координаты этих точек.
, также координаты этих точек.
10. Найти отношение, в котором каждая из координатных плоскостей делит отрезок АВ: А(2; –1; 7), В(4; 5; –2).
11. Дан тетраэдр ОАВС. Написать формулы преобразования координат точек при переходе от системы координат 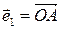 ,
,  ,
,  к системе О¢=А,
к системе О¢=А, 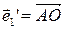 ,
,  ,
, 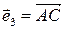 .
.
12. Найти формулы преобразования при переходе от системы Oxyz к системе Ox’y’z’, если начало новой системы координат совпадает с началом О, ось Oz’ совпадает с осью Oz, лучи Ox’ и Oy’ являются соответственно биссектрисами углов xOz и yOz и новые координатные векторы являются единичными.
Занятие № 3.
Тема: Векторное произведение векторов.
Дата добавления: 2014-12-30; просмотров: 384; Мы поможем в написании вашей работы!; Нарушение авторских прав |