V. Задачи для самостоятельной работы. 1. Векторы и взаимно перпендикулярны

1. Векторы 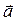и 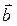взаимно перпендикулярны. Зная, что , вычислить: 1) ; 2) .

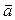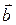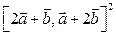2. Векторы и образуют угол . Зная, что , вычислить: 1) ; 2) ; 3) .

3. Какому условию должны удовлетворять векторы и , чтобы векторы и были коллинеарны?

4. Известно, что . Вычислите: а) 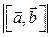, б) .

5. Вектор 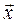, перпендикулярный векторам и , образует с осью Oy тупой угол. Зная, что , найти его координаты.

6. Вектор , перпендикулярный к оси Oz и к вектору , образует острый угол с осью Ox. Зная, что 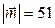, найти его координаты.

7. Даны точки А(1;2;0), В(3;0;–3) и С(5;2;6). Вычислить площадь треугольника АВС.

8. Дан треугольник АВС, в котором А(1;1;–2), В(1;1;0), С(–1;3;0). Вычислить длину его высоты AH.

9. На векторах 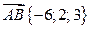и построен параллелограмм АВСД. Вычислите расстояние между прямыми: а) АВ и СД; б) AД и ВС.

10. Найдите расстояние от точки А(3;2;–2) до прямой, проходящей через точки В(1;2;3) и С(5;2;0).

11. Сила приложена к точке С(2;–1;–2). Определите величину и направляющие косинусы момента этой силы относительно начала координат.

12. Сила приложена к точке А(4;2;–3). Определить величину и направляющие косинусы момента этой силы относительно точки С(2;4;0).

13. Вычислить площадь параллелограмма АВСД, если .

14. Отрезок является высотой тетраэдра ОАВС. Найти вектор , если известны векторы .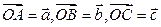

Занятие № 4.

Тема: Смешанное произведение векторов.