I. Теоретические сведения. В пространстве зададим правую прямоугольную декартову систему координат , тем самым мы определяем ориентацию в пространстве и пространство становится

В пространстве зададим правую прямоугольную декартову систему координат 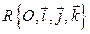, тем самым мы определяем ориентацию в пространстве и пространство становится положительно ориентированным.

Пусть 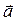и 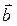- неколлинеарные векторы.

Векторным произведением вектора 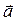на вектор 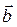называется вектор такой что:

1) . Длина вектора равна произведению длин векторов и 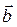на синус угла между ними.

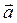2) . Вектор перпендикулярен к каждому из векторов и .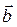

3) Тройка векторо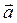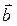в , , одинаково ориентирована с тройкой базисных векторов .

Обозначать операцию векторного произведения векторов будем следующим образом: .

Если векторы 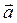и 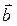– коллинеарны, то их векторным произведением называется нулевой вектор.

Геометрический смысл векторного произведения векторов состоит в том, что модуль векторного произведения векторов численно равен площади параллелограмма, построенного на векторах 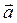и 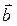как на сторонах.

Выражение векторного произведения в координатах:

, где

Свойства векторного произведения.

1.

2. (антикоммутативность)

3. (ассоциативность относительно скалярного произведения)

4. (дистрибутивность)

Свойства 3 и 4 означают линейность векторного произведения по первому аргументу, но в силу свойства 2 оно линейно и по второму аргументу.