
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
IV. Примеры решения задач. Решение. 1) По правилу параллелепипеда сложения трех некомпланарных векторов в пространстве имеем: = 2)
|
 ,
,  ,
,  . Построить каждый из следующих векторов: 1)
. Построить каждый из следующих векторов: 1) 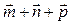 ; 2)
; 2)  ; 3)
; 3)  .
.

3)  = –
= – 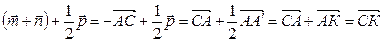 , где К – середина ребра АА'.
, где К – середина ребра АА'.
Задача 2. Даны три вектора  ,
,  ,
,  . Найти разложение вектора
. Найти разложение вектора  по базису
по базису 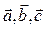 .
.
Решение.
Обозначим коэффициенты разложения вектора  по базису
по базису  через x, y, z. Тогда
через x, y, z. Тогда  . Запишем это соотношение в координатах:
. Запишем это соотношение в координатах:

Получили систему трех линейных уравнений с тремя неизвестными. Решая ее, получим x = 2, y = –3, z = 1 и  .
.
Ответ:  .
.
Задача 3. Даны три силы  ,
,  и
и  , приложенные к одной точке. Вычислить, какую работу производит равнодействующая этих сил, когда ее точка приложения, двигаясь прямолинейно, перемещается из положения М1(5;3;–7) в положение М2(4;–1;–4).
, приложенные к одной точке. Вычислить, какую работу производит равнодействующая этих сил, когда ее точка приложения, двигаясь прямолинейно, перемещается из положения М1(5;3;–7) в положение М2(4;–1;–4).
Решение.
Если вектор  изображает силу, точка приложения которой перемещается из начала в конец вектора
изображает силу, точка приложения которой перемещается из начала в конец вектора  , то работа А этой силы определяется равенством А =
, то работа А этой силы определяется равенством А =  .
.
Найдем силу  , являющуюся равнодействующей данных сил
, являющуюся равнодействующей данных сил  , т.е.
, т.е.
 ,
,  .
.
Вектор перемещения  имеет координаты
имеет координаты  .
.
Найдем скалярное произведение  в координатах:
в координатах:
 = 2∙(–1)+(–3)∙(–4)+1∙3 = 13.
= 2∙(–1)+(–3)∙(–4)+1∙3 = 13.
Ответ: А = 13.
Задача 4. Даны вершины треугольника: А(–1;–2;4), В(–4;–2;0) и С(3;–2;1). Определить его внутренний угол при вершине В.
Решение.
|

Используем формулу cos 
cos B =  . Следовательно,
. Следовательно,
 = arccos
= arccos  = 450
= 450
Ответ:  = 450.
= 450.
Задача 5. Вектор 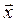 , коллинеарный вектору
, коллинеарный вектору  , образует острый угол с осью Oz. Зная, что
, образует острый угол с осью Oz. Зная, что  , найти его координаты.
, найти его координаты.
Решение.
Так как  коллинеарен вектору
коллинеарен вектору 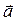 , то его координаты пропорциональны координатам
, то его координаты пропорциональны координатам 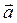 , т.е.
, т.е.  . Найдем длину вектора
. Найдем длину вектора  :
:

Учитывая, что  , получим
, получим
156,25α2 = 2500  α2 = 16
α2 = 16  α =
α =  4.
4.
Отсюда следует, что  имеет координаты
имеет координаты  или
или  .
.
Но вектор  образует острый угол с осью Oz, следовательно
образует острый угол с осью Oz, следовательно  >0, где
>0, где 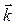 – направляющий вектор оси Oz,
– направляющий вектор оси Oz,  .
.
Найдем  <0,
<0,  >0. Учитывая, что
>0. Учитывая, что  , получим, что α = – 4 и вектор
, получим, что α = – 4 и вектор  имеет координаты
имеет координаты  .
.
Ответ:  .
.
Задача 6. Вычислите угол, который образуют единичные векторы  и
и  , если известно, что векторы
, если известно, что векторы  и
и  взаимно перпендикулярны.
взаимно перпендикулярны.
Решение.
Из того, что векторы  и
и  взаимно перпендикулярны следует, что их скалярное произведение равно 0.
взаимно перпендикулярны следует, что их скалярное произведение равно 0.

Так как  имеем:
имеем:
8+8  cos
cos 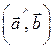 = 0
= 0
cos 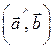 = –1,
= –1, 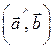 = 1800
= 1800
Ответ: π.
Дата добавления: 2014-12-30; просмотров: 987; Мы поможем в написании вашей работы!; Нарушение авторских прав |
 2)
2)  =
= 
 и
и  .
Найдем координаты этих векторов.
.
Найдем координаты этих векторов.

