КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
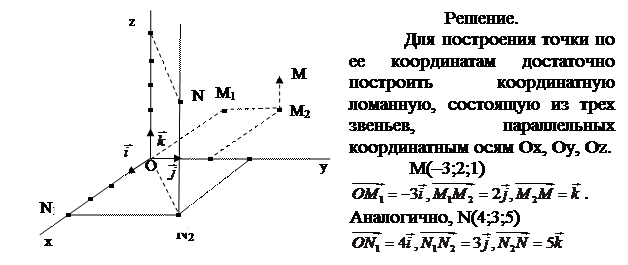
IV. Примеры решения задач. Задача 1. Построить точки М(–3;2;1) и N(4;3;5).
Задача 1. Построить точки М(–3;2;1) и N(4;3;5).
Задача 2. Даны две вершины треугольника: А(–4;–1;2), В(3;5;–16). Найти третью вершину С, зная, что середина стороны АС лежит на оси Oy, а середина стороны ВС на плоскости Oxz.
Середина Q стороны ВС лежит на плоскости Oxz 
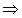yQ = 0. По формулам координат середины отрезка имеем:
, 
, 
, 
, 
, 
, 
.
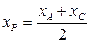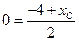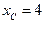
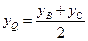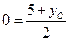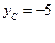
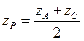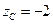Итак, точка С (4;–5;–2).
Задача 3. Прямая проходит через две точки М1(–1;6;6) и М2(3;–8;–2). Найти точку ее пересечения с координатной плоскостью Oxz.
Решение.
Точка пересечения прямой М1М2 с координатной плоскостью Oxz делит отрезок М1М2 в некотором отношении λ.
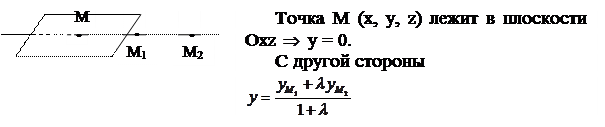
Тогда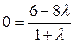 
, 
, 
.
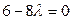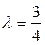Следовательно, М делит отрезок М1М2 в отношении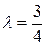 
.
По формулам деления отрезка в данном отношении получим:
, 
, 
, 
, 
.
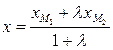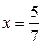
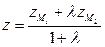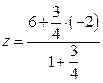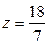Итак, точка М пересечения прямой М1М2 с плоскостью Oxz имеет координаты М (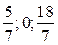 
).
Задача 4. Дан прямоугольный параллелепипед АВСДА1В1С1Д1, в котором АВ = 2, АД = 2, АА1 = 3. Найдите координаты вершин этого параллелепипеда в системе координат, если: а) начало координат совпадает с точкой А, точки В, Д, А1 принадлежат соответственно положительным полуосям координат Ox, Oy, Oz; б) она получается из системы координат пункта а) параллельным переносом в центр параллелепипеда.
АА1 = 3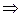 
z = 3. Следовательно, точка A1(0; 0; 3).
Под координатами точки С мы понимаем координаты ее радиус-вектора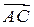 
.
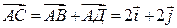
Следовательно,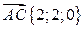 
. Значит С (2; 2; 0). Аналогично,
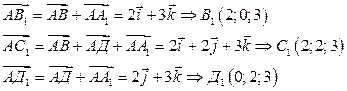
б) Формулы преобразования координат точек при параллельном переносе системы координат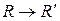 
имеют вид: 
где (x;y;z) – координаты точки относительно старой системы координат 
, (x';y';z') – координаты точки относительно новой системы координат 
, а (x0;y0;z0) – координаты начала новой системы координат относительно старой.
Координаты нового начала О' определяются следующим образом:
.
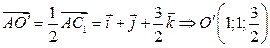Формулы преобразования для точки А имеют вид:
А(–1;–1;– 
).
Аналогично, В (2; 0; 0)R
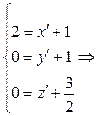В (1;–1;– 
)R';
С (2; 2; 0)R: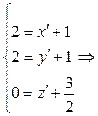 
С (1;1;– )R';
Д (0; 2; 0)R: 
Д (–1;1;– )R'.
Точка С1 – симметрична точке А относительно О' 
С1 (1;1;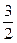 
). Аналогично, Д1 – симметрична В относительно О' 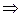Д1(–1;1; 
)
В1 – симметрична Д относительно О' 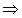В1 (1;–1; 
)
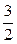А1 – симметрична С относительно О' 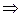А1 (–1;–1; 
).
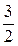Дата добавления: 2014-12-30; просмотров: 304; Мы поможем в написании вашей работы!; Нарушение авторских прав |