V. Задачи для самостоятельной работы. 1. Проверить коллинеарность векторов и

1. Проверить коллинеарность векторов и . Установить, какой из них длиннее другого и во сколько раз, как они направлены – в одну или в противоположные стороны.

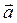2. Два вектора и приложены к одной точке. Определить координаты вектора , направленного по биссектрисе угла между векторами и 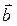, при условии, что .

3. Даны три вектора , , . Найти разложение по базису .

4. Даны неколлинеарные векторы 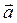и 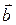. При каких значениях α и β для векторов выполняется равенство ?

5. Найдите координаты вектора 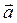, если известны его длина и углы и , которые он образует с векторами базиса ; ; а) , , , ; б) , , , ; в) , , , .

6. Доказать, что вектор перпендикулярен к вектору .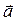

7. Найдите угол между векторами 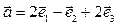и , если , , , , и взаимно-перпендикулярны.

8. Треугольник АВС задан векторами и . Найдите длины медиан АМ и ВР треугольника и угол между ними.

9. Вычислить, какую работу производит сила , когда ее точка приложения, двигаясь прямолинейно, перемещается из положения А(2;–3;5) в положение В(3;–2;–1).

10. Даны вершины треугольника А(3;2;–3), В(5;1;–1) и С(1;–2;1). Определить его внешний угол при вершине А.

11. Найти вектор , коллинеарный вектору и удовлетворяющий условию .

12. Даны три вектора: . Вычислить пр .

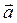13. Даны точки А(–2;3;–4), В(3;2;5), С(1;–1;2), Д(3;2;–4). Вычислить пр .

Занятие № 2.

Тема: Системы координат в пространстве.