
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
IV. Примеры решения задач.
Задача 1. Даны векторы 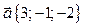 и
и 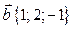 . Найти координаты векторных произведений: 1)
. Найти координаты векторных произведений: 1) 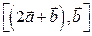 ; 2)
; 2)  .
.
Решение.
Воспользуемся свойствами векторного произведения:
1) 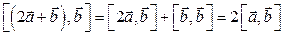
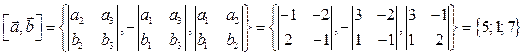 . Следовательно,
. Следовательно, 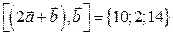 .
.
2) 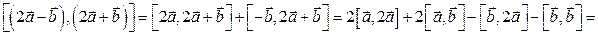
 .
.
Следовательно, 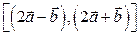 =
= 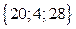 .
.
Задача 2. Найдите вектор 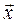 , зная, что он перпендикулярен векторам
, зная, что он перпендикулярен векторам 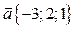 ,
, 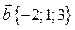 и удовлетворяет условию
и удовлетворяет условию 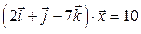 .
.
Решение.
Вектор 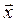 перпендикулярен векторам
перпендикулярен векторам 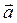 и
и 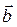 , значит он коллинеарен векторному произведению
, значит он коллинеарен векторному произведению 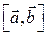 . Вычислим координаты векторного произведения:
. Вычислим координаты векторного произведения:
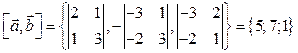 .
.
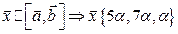 .
.
Найдем скалярное произведение векторов:
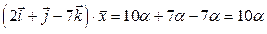
С другой стороны 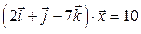 . Следовательно, имеем
. Следовательно, имеем 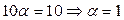 . Тогда
. Тогда 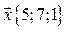 .
.
Задача 3. Векторы  и
и 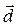 связаны соотношениями
связаны соотношениями 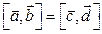 ,
,  . Доказать коллинеарность векторов
. Доказать коллинеарность векторов 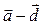 и
и 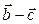 .
.
Решение.
Два вектора коллинеарны тогда и только тогда, когда их векторное произведение равно нулю.
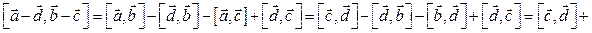
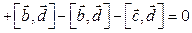 . Следовательно, векторы
. Следовательно, векторы 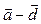 и
и 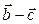 – коллинеарны.
– коллинеарны.
Задача 4. Даны вершины треугольника А (1;-1;2), В (5;-6;2) и С (1;3;-1). Вычислить длину его высоты, опущенной из вершины В на АС.

Найдем 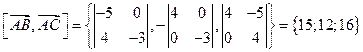 .
.
 .
.
С другой стороны, 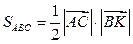
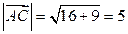 . Тогда,
. Тогда, 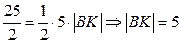 .
.
Ответ: h = 5.
Задача 5. Даны векторы 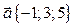 и
и 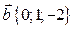 . Вычислите площадь параллелограмма, для которого векторы
. Вычислите площадь параллелограмма, для которого векторы 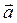 и
и 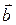 являются диагоналями.
являются диагоналями.

Выразим стороны параллелограмма АД и АВ через векторы 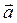 и
и 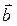 .
.
 ;
;  .
.
Площадь параллелограмма вычислим по формуле: 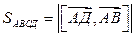 .
.
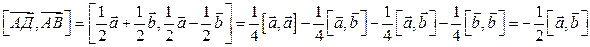 .
.
Найдем 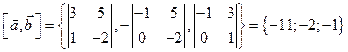 .
.
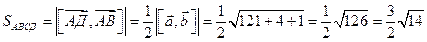 .
.
Ответ: 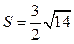 .
.
Задача 6. Сила  приложена к точке М0(4;-2;3). Определить момент этой силы относительно точки А(3;2;–1).
приложена к точке М0(4;-2;3). Определить момент этой силы относительно точки А(3;2;–1).
Решение.
Если вектор  изображает силу, приложенную к какой-нибудь точке М0, а вектор
изображает силу, приложенную к какой-нибудь точке М0, а вектор 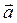 идет из некоторой точки А в точку М0, то вектор
идет из некоторой точки А в точку М0, то вектор 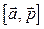 представляет собой момент
представляет собой момент 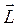 силы
силы  относительно точки А.
относительно точки А.
Найдем координаты 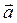 и
и 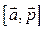 .
.
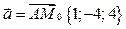 .
.
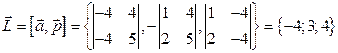 .
.
Следовательно, момент силы равен вектору 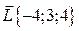 .
.
Дата добавления: 2014-12-30; просмотров: 350; Мы поможем в написании вашей работы!; Нарушение авторских прав |