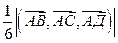КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
III. Примеры решения задач. Задача 1. Вычислите смешанное произведение векторов , , : а)
Задача 1. Вычислите смешанное произведение векторов 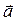 ,
, 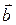 ,
,  : а)
: а) 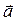 = 3
= 3  + + 2
+ + 2 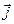 – 5
– 5 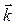 ,
, 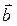 =
=  –
– 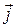 ,
,  = 2
= 2 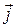 – 4
– 4 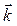 ; б)
; б)  .
.
Решение.
а) 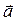 = 3
= 3  + 2
+ 2 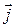 – 5
– 5 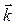 , следовательно,
, следовательно, 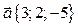 .
.
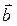 =
=  –
– 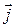
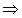
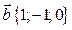 ;
;  = 2
= 2 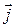 – 4
– 4 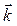
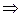
 .
.
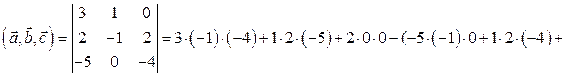
+  = 12 – 10 + 8 = 10.
= 12 – 10 + 8 = 10.
б) 
+ 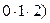
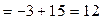 .
.
Задача 2. Установить, компланарны ли векторы 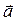 ,
, 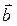 ,
,  , если:
, если:
а)  ;
;
б) 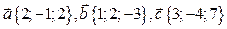 .
.
Решение.
Воспользуемся достаточным условием компланарности трех векторов:
а) 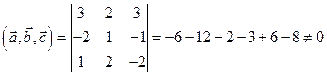 . Векторы
. Векторы 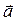 ,
, 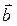 ,
,  не компланарны.
не компланарны.
б)  . Векторы
. Векторы 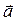 ,
, 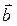 ,
, 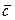 компланарны.
компланарны.
Задача 3. Доказать, что четыре точки А(1;2;–1), В(0;1;5), С(–1;2;1), Д(2;1;3) лежат в одной плоскости.
Решение:
Четыре точки А, В, С, Д лежат в одной плоскости тогда и только тогда, когда векторы  ,
, 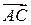 и
и 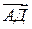 – компланарны.
– компланарны.
 – 2 = 0. Векторы компланарны. Следовательно, точки А, В, С, Д лежат в одной плоскости.
– 2 = 0. Векторы компланарны. Следовательно, точки А, В, С, Д лежат в одной плоскости.
Задача 4. Дан тетраэдр АВСД, в котором А(–1;1;1), В(0;5;–3), С(–1;4;–2).
Найдите координаты точки Д, если известно, что она лежит на оси Oz, а объем тетраэдра равен 7.

V = 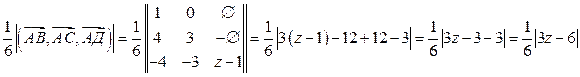
Но объем тетраэдра равен 7, следовательно,
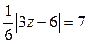 ,
, 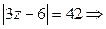
3z – 6 = 42 или 3z – 6 = – 42
3z = 48 3z = – 36
z = 16 z = – 12
Ответ: Д(0;0;16) или Д(0;0;–12).
Задача 5. Найти длину вектора ДН тетраэдра АВСД, вершины которого находятся в точках А(2;–4;5), В(–1;–3;4), С(5;5;–1), Д(1;–2;2).
|

Векторы имеют следующие координаты:  .
.
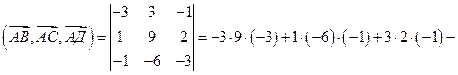
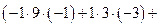
+ 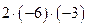 ) = 81 + 6 – 6 – 9 + 9 – 36 = 45.
) = 81 + 6 – 6 – 9 + 9 – 36 = 45.
Следовательно, Vтетр = 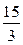 .
.
Вычислим теперь площадь основания тетраэдра, т.е. площадь треугольника АВС, используя геометрический смысл операции векторного произведения векторов:
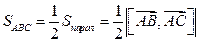

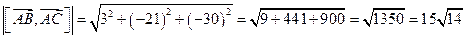

Отсюда, ДН = 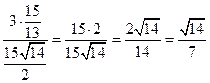 .
.
Ответ: 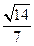 .
.
Дата добавления: 2014-12-30; просмотров: 468; Мы поможем в написании вашей работы!; Нарушение авторских прав |
 , где
, где 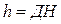 Отсюда следует, что
Отсюда следует, что 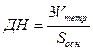 Вычислим объем тетраэдра, используя геометрический смысл смешанного произведения векторов:
Vтетр =
Вычислим объем тетраэдра, используя геометрический смысл смешанного произведения векторов:
Vтетр =