III. Примеры решения задач. Задача 1. Написать уравнение плоскости, проходящей через: а) точку М(3;-1;-5) параллельно векторам и ; б) три точки М(1;1;1)

Задача 1. Написать уравнение плоскости, проходящей через: а) точку М(3;-1;-5) параллельно векторам и ; б) три точки М(1;1;1), К(2;0;-1), Р(3;4;5). Указать их расположение относительно системы координат.

Решение.

а) Воспользуемся каноническим уравнением плоскости и преобразуем его: ;

;

;

Получим уравнение плоскости:

.

Так как все коэффициенты в уравнении плоскости отличны от нуля, то плоскость пересекает все три оси координат и не проходит через начало.

б) Воспользуемся уравнением плоскости, проходящей через три точки:

.

Преобразуем его:

;

Получим уравнение плоскости:

Плоскость пересекает все три оси координат и не проходит через начало.

Задача 2. Напишите уравнение плоскости, проходящей через точку М(2;–1;4) перпендикулярно плоскостям , .

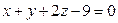Решение.

Векторы нормалей и данных плоскостей параллельны искомой плоскости и не коллинеарны, так как их соответствующие координаты не пропорциональны. Воспользуемся уравнением плоскости, заданной точкой и направляющими векторами:

,

,

.

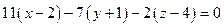Уравнение искомой плоскости имеет вид: .

Задача 3. Составить уравнение плоскости, проходящей через середину отрезка с концами в точках М₁(3;–1;2) и М₂(4;–2;–1) перпендикулярно к нему.

Решение.

Середина отрезка, точка М имеет координаты:

, , , .

Вектор 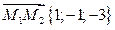перпендикулярен плоскости по условию задачи, т.е. является вектором нормали плоскости. Воспользуемся уравнением плоскости в прямоугольно декартовой системе координат:

,

.

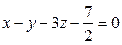Уравнение искомой плоскости имеет вид: .

Задача 4. Составить уравнение плоскости, параллельной вектору и отсекающей на координатных осях Ox и Oy отрезки а = 3, b = –2.

Решение.

Воспользуемся уравнением плоскости «в отрезках»:

.

Преобразуем это уравнение:

.

Плоскость параллельна вектору , следовательно, используя необходимое и достаточное условия параллельности вектора плоскости, заданной общим уравнением, получим:

Тогда уравнение искомой плоскости имеет вид:

,

.

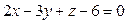Задача 5. Составить уравнение касательной плоскости к сфере в точке М₀(0;1;3).

Решение.

Точка М₀(0;1;3) принадлежит сфере, т.к. ее координаты удовлетворяют уравнению сферы и она принадлежит касательной плоскости по условию задачи, следовательно, точка М₀ является точкой касания сферы и плоскости. По свойству касательной плоскости к сфере имеем, что радиус, проведенный в точку касания перпендикулярен касательной плоскости, т.е. является вектором нормали к плоскости.

Центр сферы имеет координаты О(2;3;-1), тогда . Воспользуемся уравнением плоскости в прямоугольно декартовой системе координат:

,

.

Уравнение искомой плоскости имеет вид: .