
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
III. Примеры решения задач.
Задача 1. Определить взаимное расположение плоскостей:
а)  и
и  ;
;
б)  и
и  ;
;
в)  и
и  .
.
Решение.
а) Составим основную и расширенную матрицы
 и
и 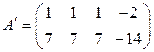 .
.
Найдем ранг этих матриц:



 .
.
Так как  и
и  , то плоскости П1 и П2 совпадают.
, то плоскости П1 и П2 совпадают.
б) 
 ,
, 
 .
.
Следовательно, плоскости П1 и П2 параллельны.
в) 
 , следовательно плоскости П1 и П2 пересекаются по прямой.
, следовательно плоскости П1 и П2 пересекаются по прямой.
Задача 2. Через точку М0(–5;16;12) проведены две плоскости: одна из них содержит ось абсцисс, другая – ось ординат. Вычислить угол между этими двумя плоскостями.
Решение.
Составим уравнение плоскости П1, которая проходит через точку М0 и содержит ось абсцисс. Плоскость П1 задается двумя точками М0(–5;16;12) и О(0;0;0) и направляющим вектором  . Следовательно, уравнение плоскости П1 имеет вид:
. Следовательно, уравнение плоскости П1 имеет вид:
 .
.
Или П1:  .
.
Аналогично составим уравнение плоскости П2, проходящей через точку М0 и содержащей ось ординат (П2: М0, О,  ).
).
П2:  или П2:
или П2:  .
.
Тогда  .
.
Угол  между плоскостями П1 и П2 равен
между плоскостями П1 и П2 равен  .
.
Задача 3. Составить уравнение плоскости, которая проходит через точку М1(3;-2;-7) параллельно плоскости 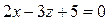 .
.
Решение.
Искомая плоскость П имеет уравнение вида  . Так как точка М1
. Так как точка М1  П, то ее координаты удовлетворяют этому уравнению:
П, то ее координаты удовлетворяют этому уравнению:
 . Отсюда Д1 = –27.
. Отсюда Д1 = –27.
Тогда П:  .
.
Задача 4. Напишите уравнение плоскости, проходящей через линию пересечения плоскостей  и
и  и через точку М(3;2;1).
и через точку М(3;2;1).
Решение.
Так как искомая плоскость П проходит через линию пересечения двух плоскостей П1 и П2, то она принадлежит пучку плоскостей, образованному плоскостями П1 и П2. Уравнение пучка плоскостей имеет вид:
 , где
, где  .
.
Тогда уравнение любой плоскости пучка и в частности плоскости П имеет вид:
 .
.
Точка М(3;2;1)  П, следовательно, ее координаты удовлетворяют уравнению плоскости:
П, следовательно, ее координаты удовлетворяют уравнению плоскости:
 ,
,
 .
.
Отсюда имеем, что уравнение плоскости
П:  ,
,
 или
или  .
.
Задача 5. Напишите уравнение плоскости, проходящей через точку М(2;–1;4) перпендикулярно плоскостям  и
и 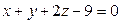 .
.
Решение.
Искомая плоскость 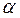 перпендикулярна плоскости
перпендикулярна плоскости  и
и  . Следовательно, векторы нормали к плоскостям
. Следовательно, векторы нормали к плоскостям  и
и  будут параллельны плоскости
будут параллельны плоскости  . Таким образом, плоскость
. Таким образом, плоскость 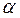 определяется точкой М(2;-1;4) и двумя направляющими векторами:
определяется точкой М(2;-1;4) и двумя направляющими векторами:  и
и  .
.
Уравнение плоскости  имеет вид:
имеет вид:
 :
:  ,
,
 ,
,
 .
.
Итак, плоскость 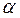 задается уравнением
задается уравнением  .
.
Задача 6. Определить, при каких значениях a и b плоскости  ,
,  ,
,  :
:
1) имеют одну общую точку;
2) проходят через одну прямую;
3) пересекаются по трем различным параллельным прямым.
Решение.
1) Три плоскости, заданные относительно аффинной системы координат общими уравнениями:

имеют одну общую точку тогда и только тогда, когда система, составленная из уравнений этих плоскостей, имеет единственное решение (Рис. 1).
Система имеет единственное решение  определитель
определитель
 .
.

 .
.
Итак, плоскости имеют одну общую точку при 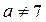 .
.
2) Введем обозначения:
 ,
, 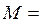
 ,
,  - векторы нормали соответственно к плоскостям
- векторы нормали соответственно к плоскостям  .
.
Плоскости  и
и  проходят через прямую, если
проходят через прямую, если 
 ,
, 
 и векторы
и векторы  - не коллинеарны (Рис. 2).
- не коллинеарны (Рис. 2).














При 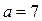 и
и  векторы нормали к плоскостям имеют координаты:
векторы нормали к плоскостям имеют координаты:  ,
, 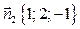 ,
,  . Нетрудно заметить, что
. Нетрудно заметить, что  не параллелен
не параллелен  не параллелен
не параллелен  . Следовательно, плоскости
. Следовательно, плоскости 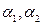 и
и  пересекаются по прямой при
пересекаются по прямой при  и
и  .
.
3) Плоскости 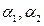 и
и  пересекаются по трем различным прямым, если
пересекаются по трем различным прямым, если 
 ,
, 
 и векторы
и векторы  - не коллинеарны.
- не коллинеарны.

Дата добавления: 2014-12-30; просмотров: 1486; Мы поможем в написании вашей работы!; Нарушение авторских прав |