I. Теоретические сведения. Нормальным уравнением плоскости называется уравнение

Нормальным уравнением плоскости называется уравнение

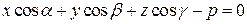, (1)

где 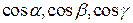– направляющие косинусы нормали плоскости, p – расстояние плоскости от начала координат.

знак нормирующего множителя берется противоположным знаку свободного члена Д уравнения (2).

Замечание: Если Д = 0, то знак нормирующего множителя можно выбрать любой.

Если в левую часть уравнения плоскости в нормальной форме подставить координаты любой точки пространства, то получится число, с точностью до знака, равное расстоянию от этой точки до плоскости.

Формула для нахождения расстояния от точки М₀(x₀,y₀,z₀) до плоскости П: имеет вид:

.

Геометрический смысл знака многочлена состоит в следующем:

неравенство задает то полупространство относительно плоскости , которому принадлежит конец вектора нормали этой плоскости, отложенного от некоторой точки плоскости;

неравенство задает другое полупространство относительно указанной плоскости.

Дата добавления: 2014-12-30; просмотров: 16; Нарушение авторских прав