IV. Примеры решения задач. Задача 1. Определить координаты нескольких точек, лежащих на прямых: а) ; б) ; в)

Задача 1. Определить координаты нескольких точек, лежащих на прямых: а) ; б) ; в) . Какие из точек М₁(–2;–9;7), М₂(–3;0;4), М₃(3;1;1) принадлежат этим прямым?

Решение.

а) Положим x = 1 и подставим это значение в уравнение прямой, получим y = 0, z = 4.

Точка М(1;0;4) принадлежит прямой.

Положим x = 3 и подставим это значение в уравнение прямой, получим y = 6, z = 2.

Точка N(3;6;2) принадлежит прямой.

б) Из первого уравнения выразим параметр : и подставим найденное выражение в оставшиеся уравнения: .

Положив x = 3, получим y = 0, z = 5.

Точка М(3;0;5) принадлежит прямой.

Если , то , , .

Точка N(7;6;5) принадлежит прямой.

в) Решим систему двух уравнений с тремя неизвестными. Из первого уравнения системы имеем x = 3.

Положив y = 2, получим z = 0.

Точка М(3;2;0) принадлежит прямой.

Положив y = –3, получим z = 5.

Точка N(3;–3;5) принадлежит прямой.

Проверим, какие из точек М₁, М₂, М₃ принадлежат данным прямым. Подставим координаты точки М₁ в уравнение прямой а): . Получим верное равенство, значит М₁ принадлежит прямой а). Аналогично проверяем, что точка М₃ принадлежит прямой в), а точка М₂ не принадлежит ни одной из этих прямых.

Задача 2. Даны вершины треугольника А(2;3;–1), В(1;–2;0) и С(–3;2;2). Составить канонические уравнения медианы AP.

Решение.

Следовательно, P(–1;0;1). Так как медиана проходит через точки A и P, то подставив координаты этих точек в уравнения прямой, проходящей через две точки, получим:

или .

Задача 3. Через точку М₀(2;–3;–4) провести прямую, параллельную прямой

Решение.

Найдем направляющий вектор данной прямой:

, т.е. .

Этот же вектор будет направляющим и для искомой прямой, т.к. она параллельна данной прямой, поэтому ее канонические уравнения запишутся в виде:

.

Параметрические уравнения этой прямой имеют вид:

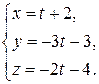
Задача 4. Привести уравнения прямой к каноническому и параметрическому виду.

Решение.

Определим координаты какой-нибудь точки данной прямой. Пусть, например, z = 0, тогда

Отсюда x = 27, y = 15. Точка М(27;15;0) принадлежит данной прямой. Определим координаты направляющего вектора прямой , , .

или .

В качестве направляющего вектора прямой можно взять любой вектор коллинеарный , в частности .

Запишем канонические уравнения прямой:

.

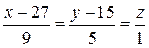Параметрические уравнения прямой:

Задача 5. Даны вершины треугольника A(1;–1;3), B(3;–4;9), C(–5;11;7). Найти канонические уравнения биссектрисы его внутреннего угла при вершине A.

Решение.

– орт вектора , . Найдем координаты и длины векторов и :

.

Найдем координаты векторов и :

, .

Тогда 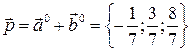. В качестве направляющего вектора биссектрисы угла BAC можно взять любой вектор коллинеарный , в частности, вектор . Биссектриса AL треугольника ABC задана точкой A(1;–1;3) и направляющим вектором . Составим канонические уравнения прямой AL:

.