
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
IV. Примеры решения задач. Задача 1. Определите взаимное расположение следующих пар прямых:
Задача 1. Определите взаимное расположение следующих пар прямых:
а)  :
:  и
и  :
: 
б)  :
:  и
и  :
: 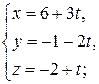
в)  :
:  и
и  :
: 
Решение.
а) Прямые  и
и  заданы общими уравнениями, поэтому найдем сначала координаты направляющих векторов этих прямых
заданы общими уравнениями, поэтому найдем сначала координаты направляющих векторов этих прямых  и
и  и координаты какой-нибудь точки М1, принадлежащей прямой
и координаты какой-нибудь точки М1, принадлежащей прямой  и точки М2, принадлежащей прямой
и точки М2, принадлежащей прямой  .
.
 :
:  ,
, 

 , т.е.
, т.е. 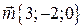 .
.
Найдем координаты какой-нибудь точки М1 прямой  . Пусть, например, y1 = 0, тогда x1 = 0 и z1 = 4. Т.е. точка имеет координаты М1(0;0;4).
. Пусть, например, y1 = 0, тогда x1 = 0 и z1 = 4. Т.е. точка имеет координаты М1(0;0;4).
 :
:  ,
, 

 , т.е.
, т.е.  .
.
Найдем какую-нибудь точку М2, принадлежащую прямой  . Пусть, например, z = 1. Тогда x = 7, y = 2, т.е. М2(7;2;1).
. Пусть, например, z = 1. Тогда x = 7, y = 2, т.е. М2(7;2;1).
Найдем определитель:
 .
.
Отсюда следует, что прямые  и
и  скрещиваются.
скрещиваются.
б)  :
:  , М1(1;7;3)
, М1(1;7;3)
 :
:  , М2(6;–1;–2)
, М2(6;–1;–2)
Найдем определитель:
 .
.
Следовательно, прямые лежат в одной плоскости. Векторы  и
и  – не коллинеарны, значит прямые
– не коллинеарны, значит прямые  и
и  – пересекаются.
– пересекаются.
в)  :
:  , М1(0;0;–3)
, М1(0;0;–3)
 :
:  , т.е.
, т.е.  .
.
Найдем какую-нибудь точку М2, принадлежащую прямой  . Пусть, например, z = –2. Тогда x = 9, y = 5. Точка М2(9;5;–2) принадлежит прямой
. Пусть, например, z = –2. Тогда x = 9, y = 5. Точка М2(9;5;–2) принадлежит прямой  .
.
Найдем определитель:
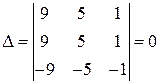 .
.
Следовательно, прямые  и
и  лежат в одной плоскости. Векторы
лежат в одной плоскости. Векторы  и
и  – коллинеарны, значит прямые
– коллинеарны, значит прямые  и
и  либо параллельны, либо совпадают. Вектор
либо параллельны, либо совпадают. Вектор  коллинеарен вектору
коллинеарен вектору  и вектору
и вектору  , поэтому прямые
, поэтому прямые  и
и  совпадают.
совпадают.
Задача 2. Написать уравнения прямой  , проходящей посередине между параллельными прямыми
, проходящей посередине между параллельными прямыми  и
и  , заданными уравнениями:
, заданными уравнениями:  :
:  и
и  :
: 
Решение:

Для определения координат точки М2 
 положим, например, x0 = 1. Тогда,
положим, например, x0 = 1. Тогда,  получим z0 = 0, y0 = –1. Отсюда М2(1;–1;0).
получим z0 = 0, y0 = –1. Отсюда М2(1;–1;0).
Вычислим координаты середины отрезка М1М2:
 ;
;  ;
; 
 А(3;
А(3;  ;
;  ).
).
Уравнение прямой  , проходящей через точку А с направляющим вектором
, проходящей через точку А с направляющим вектором  имеет вид:
имеет вид:
 .
.
Задача 3. Найти угол между прямыми  и
и 
Решение.
Найдем направляющие векторы этих прямых:
 ,
,
 .
.
Косинус угла между данными прямыми:
 ,
,
 .
.
Задача 4. Составить канонические уравнения прямой, лежащей в плоскости XOZ, проходящей через начало координат и перпендикулярной к прямой  .
.
Решение.
Пусть  – направляющий вектор искомой прямой
– направляющий вектор искомой прямой  . Прямая
. Прямая  лежит в плоскости XOY, поэтому проекция вектора
лежит в плоскости XOY, поэтому проекция вектора  на ось Oy равна нулю, т.е.
на ось Oy равна нулю, т.е.  = 0. Из условия перпендикулярности прямой
= 0. Из условия перпендикулярности прямой  данной прямой
данной прямой  следует, что их направляющие векторы
следует, что их направляющие векторы  и
и  перпендикулярны, т.е.
перпендикулярны, т.е.  .
.
Поскольку направляющий вектор  задается с точностью до множителя, можно одну из координат выбрать произвольно. Например, положим
задается с точностью до множителя, можно одну из координат выбрать произвольно. Например, положим  = 3, получим
= 3, получим  = –1, следовательно,
= –1, следовательно,  .
.
Искомая прямая  проходит через начало координат О(0;0;0), поэтому ее канонические уравнения:
проходит через начало координат О(0;0;0), поэтому ее канонические уравнения:
 .
.
Задача 5. Доказать, что прямые  и
и  пересекаются. Найти точку их пересечения.
пересекаются. Найти точку их пересечения.
Решение.
Точка М1(1;–2;0) принадлежит первой прямой, а М2(–1;–11;–6) – второй. Найдем смешанное произведение векторов  и направляющих векторов данных прямых
и направляющих векторов данных прямых  и
и  .
.
 .
.
Следовательно, эти векторы компланарны, и две прямые лежат в одной плоскости. Поскольку векторы  и
и  неколлинеарны (их координаты непропорциональны), то прямые не параллельны, т.е. не пересекаются.
неколлинеарны (их координаты непропорциональны), то прямые не параллельны, т.е. не пересекаются.
Найдем точку пересечения прямых. Для этого приведем уравнение одной из прямых к параметрическому виду и из уравнения второй прямой найдем значение параметра  , отвечающего точке пересечения.
, отвечающего точке пересечения.
Параметрические уравнения первой прямой имеют вид:
 ,
,  ,
,  .
.
Подставляя эти выражения для x, y, z в уравнения второй прямой, получим:
 , откуда
, откуда  .
.
Следовательно, точка пересечения имеет координаты:
 ,
,  ,
,  .
.
Ответ: (3;–3;–2).
Задача 6. Доказать, что прямые  ,
,  ,
,  и
и  ,
,  ,
,  лежат в одной плоскости, и написать уравнение этой плоскости.
лежат в одной плоскости, и написать уравнение этой плоскости.
Решение.
Точка М1(2;0;–1) принадлежит первой прямой, а точка М2(7;2;0) второй. Найдем смешанное произведение векторов  и направляющих векторов прямых
и направляющих векторов прямых  и
и  .
.
 .
.
Следовательно, векторы компланарны и две прямые лежат в одной плоскости. Векторы  и
и  – коллинеарны (их координаты пропорциональны). Следовательно, прямые параллельны.
– коллинеарны (их координаты пропорциональны). Следовательно, прямые параллельны.

 ,
,  . Поскольку координаты векторов
. Поскольку координаты векторов  и
и  – непропорциональны, эти векторы неколлинеарны. Воспользуемся уравнением плоскости, заданной точкой М1 и направляющими векторами
– непропорциональны, эти векторы неколлинеарны. Воспользуемся уравнением плоскости, заданной точкой М1 и направляющими векторами  и
и  :
:
 ,
,
 .
.
Отсюда,  – уравнение искомой плоскости.
– уравнение искомой плоскости.
Дата добавления: 2014-12-30; просмотров: 1696; Мы поможем в написании вашей работы!; Нарушение авторских прав |