I. Теоретические сведения. 1.Поверхности вращения.

1.Поверхности вращения.

Определение. Поверхностью вращения называется поверхность, образованная вращением плоской линии g вокруг оси, лежащей в плоскости этой линии.

Пусть , тогда ее можно задать уравнениями

Уравнение поверхности, образованной вращением линии g вокруг оси Oz будет иметь вид:

(1)

2. Цилиндрические поверхности.

Пусть в пространстве дана некоторая плоская линия g и вектор , не параллельный плоскости этой линии.

Определение. Цилиндрической поверхностью называется множество точек пространства, лежащих на прямых параллельных данному вектору и пересекающих данную линию g.

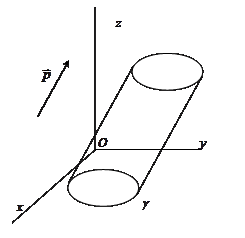Линия g называется направляющей цилиндрической поверхности, прямые называются образующими.

Рассмотрим частный случай: направляющая линия g лежит в плоскости xOy: и задается уравнениями: а направляющий вектор образующих имеет координаты , .

В этом случае уравнение цилиндрической поверхности имеет вид

. (2)