IV. Примеры решения задач. Задача 1. Написать уравнение конической поверхности, вершина которой находится в начале координат, а направляющая задана уравнениями

Задача 1. Написать уравнение конической поверхности, вершина которой находится в начале координат, а направляющая задана уравнениями

Решение.

Пусть точка M(x, y, z) – произвольная точка конической поверхности. Проведем через эту точку образующую l, она пересечет направляющую в точке . Запишем канонические уравнения прямой l, как уравнения прямой, проходящей через точку N и вершину конуса О(0, 0, 0)

,

.

Или

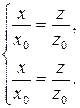
Выразим из последней системы и 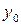: , 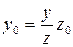. Т.к. точка N лежит на направляющей конической поверхности, то ее координаты должны удовлетворять уравнениям направляющей:

(3)

Подставим найденные выражения во второе уравнение системы (3)

,

,

,

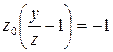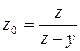. (4)

Тогда

, . (5)

Подставляем (4) и (5) в первое уравнение системы (3)

,

,

.

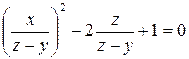Полученное уравнение является искомым уравнением конической поверхности.