IV. Примеры решения задач. Задача 1. Написать каноническое уравнение эллипсоида, который проходит через точку и пересекает плоскость xOy по эллипсу .

Задача 1. Написать каноническое уравнение эллипсоида, который проходит через точку и пересекает плоскость xOy по эллипсу .

Решение.

Каноническое уравнение эллипсоида имеет вид 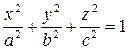. Плоскость xOy пересекает эллипсоид по эллипсу . По условию это уравнение имеет вид . Следовательно, , . Таким образом, уравнение эллипсоида принимает вид

. (8)

По условию точка принадлежит эллипсоиду, следовательно ее координаты удовлетворяют уравнению эллипсоида. Подставляя координаты точки M в уравнение (8), получаем

,

откуда

, .

Следовательно, искомое уравнение эллипсоида имеет вид

.

Ответ: .

Задача 2. Установить, что плоскость пересекает эллипсоид по эллипсу, найти его полуоси и вершины.

Решение.

Координаты общих точек эллипсоида и плоскости удовлетворяют системе уравнений:

Выразив из первого уравнения z и подставив его во второе, получим

,

.

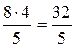Последнее уравнение определяет в плоскости , эллипс, вершина которого лежит на оси Oz, большая полуось равна , а малая полуось – . Следовательно, вершины этого эллипса имеют координаты , , , .