I. Теоретические сведения.

1. Однополостный гиперболоид.

Определение. Однополостным гиперболоидом называется множество точек пространства, координаты которых в некоторой системе координат удовлетворяют следующему уравнению

. (1)

Уравнение (1) называется каноническим уравнением однополостного гиперболоида.

Из уравнения гиперболоида можно получить ряд свойств:

1) Однополостный гиперболоид фигура неограниченная.

2) Плоскости симметрии однополостного гиперболоида: xOy, yOz, xOz;

оси симметрии однополостного гиперболоида: Ox, Oy, Oz;

центр симметрии однополостного гиперболоида: начало координат.

3) Вершинами поверхности называются точки пересечения с осями симметрии. Вершины однополостного гиперболоида: 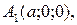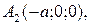(точки пересечения с осью Ox) 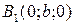, (точки пересечения с осью Oy), ось Oz однополостный гиперболоид не пересекает.

Исследование однополостного гиперболоида методом сечений.

1) Сечение плоскостью a, параллельной плоскости .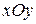

(2)

Или

. (3)

Из уравнении (3) следует, что при всех значениях h сечением однополостного гиперболоида является эллипс.

2) Сечение плоскостью b, параллельной плоскости .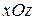

(4)

Или

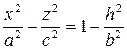. (5)

а) Если , то линия пересечения гипербола, действительная ось которой параллельна оси Ох. В частности, если , то 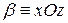, и в сечении мы получаем гиперболу ;

б) если 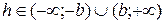, то линия пересечения гипербола, действительная ось которой параллельная оси Oz;

в) если 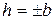, то линия пересечения пара действительных пересекающихся прямых.

3) Сечение плоскостью g, параллельной плоскости .

(6)

Или

. (7)

а) Если 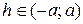, то линия пересечения гипербола, действительная ось которой параллельна оси Оy. В частности, если , то , и в сечении мы получаем гиперболу ;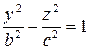

б) если 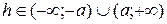, то линия пересечения гипербола, действительная ось которой параллельная оси Oz;

в) если 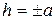, то линия пересечения пара действительных пересекающихся прямых.

2. Двуполостный гиперболоид.

Определение. Двуполостным гиперболоидом называется множество точек пространства, координаты которых в некоторой системе координат удовлетворяют следующему уравнению

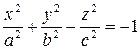. (8)

Уравнение (8) – каноническое уравнение двуполостного гиперболоида.

Из уравнения гиперболоида можно получить ряд свойств:

1) Внутри полосы, ограниченной плоскостями , точек гиперболоида нет;

3) Плоскости симметрии двуполостного гиперболоида: xOy, yOz, xOz;

оси симметрии двуполостного гиперболоида: Ox, Oy, Oz;

центр симметрии двуполостного гиперболоида: начало координат.

3) Вершины двуполостного гиперболоида: (точки пересечения с осью Oz), оси Ox и Oy двуполостный гиперболоид не пересекает.

Исследование двуполостного гиперболоида методом сечений.

1) Сечение плоскостью a, параллельной плоскости .

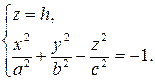(9)

Или

. (10)

а) Если 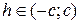, то линия пересечения мнимый эллипс;

б) если 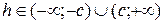, то линия пересечения эллипс;

в) если 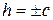, то линия пересечения пара мнимых пересекающихся прямых с действительной точкой пересечения.

2) Сечение плоскостью b, параллельной плоскости .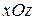

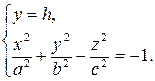(11)

Или

. (12)

При любом значении h получаем гиперболу с действительной осью параллельной оси Oz. В частности, если , то 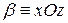, и в сечении мы получаем гиперболу ;

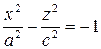3) Сечение плоскостью g, параллельной плоскости .

(13)

Или

. (14)

При любом значении h получаем гиперболу с действительной осью параллельной оси Oz. В частности, если , то , и в сечении мы получаем гиперболу .