V. Задачи для самостоятельного решения. 1) Найти уравнение параболоида с центром в начале координат, ось которого совпадает с осью Oz и который проходит через точки (1; –2; 1) и (–3; –3; 2).

1) Найти уравнение параболоида с центром в начале координат, ось которого совпадает с осью Oz и который проходит через точки
(1; –2; 1) и (–3; –3; 2).

2) Дана плоскость a и перпендикулярная к ней прямая l. Найти множество точек пространства, для каждой из которых квадрат расстояния до прямой l в три раза больше расстояния до плоскости a.

3) Напишите каноническое уравнение гиперболического параболоида с вершиной в начале координат, ось которого совпадает с осью Oy, если известно, что он проходит через точк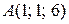и и .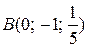

4) Доказать, что эллиптический параболоид имеет одну общую точку с плоскостью 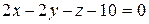, и найти ее координаты.

5) Найдите прямолинейные образующие параболоида 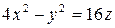, проходящие через точку М(2; 0; 1).

6) Убедившись, что точка А(–2; 0; 1) лежит на гиперболическом параболоиде 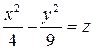, определить острый угол, образованный его прямолинейными образующими, проходящими через точку А.

7) Найдите прямолинейные образующие гиперболоида 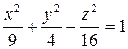, проходящие через точку (6; 2; 8).

8) Найдите прямолинейные образующие гиперболоида 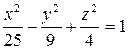, проходящие через точку (5; 3; 2).

9) На гиперболическом параболоиде 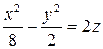найти прямолинейные образующие, параллельные плоскости .

10) Написать уравнение плоскости, параллельной плоскости 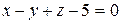и пересекающей параболоид по двум прямолинейным образующим. Найти уравнения этих образующих.

Дата добавления: 2014-12-30; просмотров: 18; Нарушение авторских прав