IV. Примеры решения задач. Задача 1. Написать каноническое уравнение однополостного гиперболоида, если он пересекает плоскость xOy по эллипсу

Задача 1. Написать каноническое уравнение однополостного гиперболоида, если он пересекает плоскость xOy по эллипсу , а плоскость yOz по гиперболе .

Решение.

Каноническое уравнение однополостного гиперболоида имеет вид . Уравнение плоскости xOy: z=0. Следовательно, уравнение линии пересечения плоскости и гиперболоида ищем как решение системы

Получаем уравнение эллипса, лежащего в плоскости xOy

.

По условию задачи этот эллипс задан уравнением . Значит, .

Проводя аналогичные рассуждения, можно получить уравнение гиперболу, получающейся в сечении гиперболоида с плоскостью yOz

.

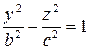По условию, это гипербола . Следовательно, .

Таким образом, искомое уравнение гиперболоида имеет вид

.

Ответ: .

Задача 2. Напишите уравнение плоскости, параллельной плоскости yOz и пересекающей однополостный гиперболоид по гиперболе, действительная полуось которой равна 1.

Решение.

Уравнение плоскости параллельной плоскости yOz имеет вид x=h. Линия пересечения этой плоскости с гиперболоидом задается системой

Откуда получаем уравнение

,

.

Последнее уравнение – это каноническое уравнение гиперболы, действительная полуось которой равна . По условию она равна 1.

,

,

,

.

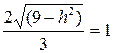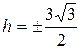Следовательно, искомая плоскость имеет уравнение .

Ответ: .