I. Теоретические сведения. Определение. Эллипсоидом называется множество точек пространства, координаты которых в некоторой системе координат удовлетворяют следующему уравнению

Определение. Эллипсоидом называется множество точек пространства, координаты которых в некоторой системе координат удовлетворяют следующему уравнению

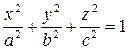. (1)

Уравнение (1) называется каноническим уравнением эллипсоида. Числа a,b,c>0 – полуоси эллипсоида.

Из уравнения эллипсоида можно получить ряд свойств:

1) Все точки эллипсоида расположены внутри прямоугольного параллелепипеда, ограниченного плоскостями , , .

2) Плоскости симметрии эллипсоида: xOy, yOz, xOz;

оси симметрии эллипсоида: Ox, Oy, Oz;

центр симметрии эллипсоида: начало координат.

3) Вершинами поверхности называются точки пересечения с осями симметрии. Вершины эллипсоида: , , , .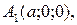

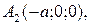
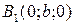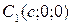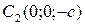Исследование эллипсоида методом сечений.

Рассмотрим сечения эллипсоида плоскостями, параллельными плоскостям симметрии.

1) Сечение плоскостью a, параллельной плоскости .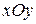

(2)

Или

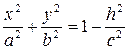. (3)

а) Если 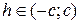, то линия пересечения эллипс, в частности, если , то , и в сечении мы получаем эллипс ;

б) если 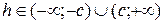, то линия пересечения мнимый эллипс;

в) если 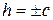, то линия пересечения пара мнимых пересекающихся прямых с действительной точкой пересечения.

2) Сечение плоскостью b, параллельной плоскости .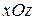

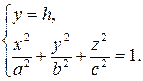(4)

Или

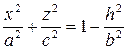. (5)

а) Если , то линия пересечения эллипс, в частности, если , то 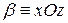, и в сечении мы получаем эллипс ;

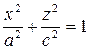б) если 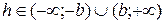, то линия пересечения мнимый эллипс;

в) если 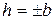, то линия пересечения пара мнимых пересекающихся прямых с действительной точкой пересечения.

3) Сечение плоскостью g, параллельной плоскости .

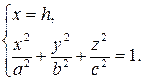(6)

Или

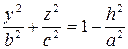. (7)

а) Если 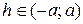, то линия пересечения эллипс, в частности, если , то 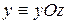, и в сечении мы получаем эллипс ;

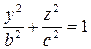б) если 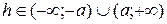, то линия пересечения мнимый эллипс;

в) если 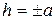, то линия пересечения пара мнимых пересекающихся прямых с действительной точкой пересечения.

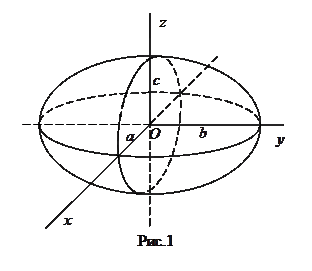
На рис.1 показаны сечения эллипсоида координатными плоскостями.