IV. Примеры решения задач. Задача 1. В плоскости yOz дана окружность с центром в точке (0; 4; 0) радиуса 1

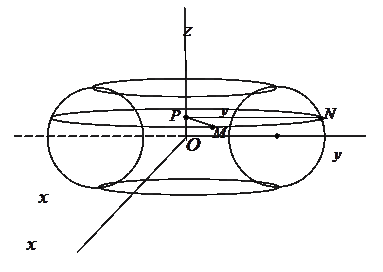
Задача 1. В плоскости yOz дана окружность с центром в точке (0; 4; 0) радиуса 1. Написать уравнение поверхности, образованной вращением данной окружности вокруг оси Oz.

Решение.

Уравнения окружности, лежащей в плоскости yOz с центром в точке (0; 4; 0) радиуса 1, имеют вид

(3)

При вращении этой окружности вокруг оси Oz получается поверхность, называемая тором. Пусть М – произвольная точка на торе. Проведем через точку М плоскость a, перпендикулярную оси вращения, т.е. оси Oz, в сечении получим окружность. Обозначим центр этой окружности P, а точку пересечения плоскости a с окружностью, образующей поверхность вращения, – N.

Обозначим координаты точки M(x, y, z), тогда P(0, 0, z), а N(0, 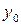, z). Так как точки M и N лежат на окружности с центром в точке P, то

,

.

Последнее равенство запишем в координатах

. (4)

Точка N лежит на окружности, при вращении которой образуется тор, значит ее координаты должны удовлетворять уравнениям (3), запишем первое уравнение системы (3)

,

,

.

Возведем последнее равенство в квадрат.

и подставим выражение для 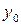из равенства (4), получим

(5)

Уравнение (5) – искомое.

Ответ: .

Задача 2. Составить уравнение цилиндрической поверхности, если направляющая лежит в плоскости xOy и имеет уравнение 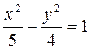, а образующие параллельны вектору {1; 2; –1}.

Решение.

Пусть точка M(x, y, z) – произвольная точка цилиндрической поверхности. Проведем через точку М образующую l, она пересекает направляющую в точке . Так как направляющая лежит в плоскости xOy, то . Составим канонические уравнения прямой l

.

Приравняем первую и вторую дроби к последней

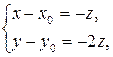
(6)

Точка N лежит на направляющей, значит ее координаты удовлетворяют ее уравнению:

.

Подставляя выражения для и 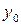из системы (6), получим

. (7)

(7) – искомое уравнение.

Ответ: .