V. Задачи для самостоятельного решения. 1. Найти точки пересечения прямой с координатными плоскостями.

1. Найти точки пересечения прямой с координатными плоскостями.

2. Какие из точек A(3;–1;–1), B(1;2;7), C(–5;14;–3) принадлежат прямой , , ?

3. Определить координаты точки, лежащей на прямой и имеющей: а) абсциссу, равную 3; б) ординату, равную –1.

4. Составить канонические уравнения прямой, проходящей через точку М₁(2;0;–3) параллельно: а) вектору ; б) прямой ; в) оси Ox; г) оси Oy; д) оси Oz.

5. Составить канонические уравнения прямой, проходящей через две данные точки: а) A₁(1;–2;1), A₂(3;1;–1); б) B₁(3;–1;0), B₂(1;0;–3); в) C₁(0;–2;3), C₂(3;–2;1).

6. Составить параметрические уравнения прямой, проходящей через точку М₁(1;–1;–3) параллельно: а) вектору ; б) прямой 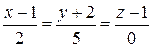; в) прямой , , .

7. Напишите параметрические уравнения прямой, проходящей через две данные точки: а) A₁(3;–1;2), B₁(2;1;1); б) A₂(1;1;–2), B₂(3;–1;0); в) A₃(2;5;3), B₃(3;–2;2).

8. Напишите канонические и параметрические уравнения прямой: а) б) в)

9. Напишите канонические уравнения прямой, проходящей через точку A(1;2;–3) параллельно прямой

10. В треугольной призме ABCA₁B₁C₁ даны вершины: A(2;–1;–1), B(5;–1;2), C(3;0;–3), A₁(6;0;–1). Напишите уравнения боковых ребер призмы.

11. Даны вершины треугольника A(2;–1;–3), B(5;2;–7) и C(–7;11;6). Составить канонические уравнения биссектрисы его внешнего угла при вершине A.

12. Даны вершины треугольника A(1;–2;-4), B(3;1;–3) и C(5;1;–7). Составить параметрические уравнения его высоты, опущенной из вершины B на противоположную сторону.

Указание: Направляющий вектор прямой BK (K – основание высоты) найти из условий: 1) , где ; 2) 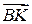ортогонален .

13. Найти канонические уравнения прямой, проходящей через точку М₀(2;1;–1) перпендикулярно плоскости .

14. Даны вершины треугольника A(3;6;–7), B(–5;2;3) и C(4;–7;–2). Составить канонические и параметрические уравнения его медианы, проведенной из вершины C и биссектрисы внутреннего угла при вершине B.

15. Составить уравнения прямой, образованной пересечением плоскости с плоскостью, проходящей через ось Ox и точку E(3;2;–5).