
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
I. Теоретические сведения. Положение прямой в пространстве однозначно определяется, если даны:
Положение прямой в пространстве однозначно определяется, если даны:
1. точка М0 и направляющий вектор  прямой;
прямой;
2. две различные точки М1 и М2 прямой;
3. две различные плоскости, пересекающиеся по этой прямой.
Основные виды уравнений прямой
1. Уравнение прямой, заданной точкой М0 и направляющим вектором  :
:

2. Уравнения прямой, проходящей через две точки М1(x1,y1,z1) и M2(x2,y2,z2):
|

3. Уравнения прямой, заданной двумя пересекающимися плоскостями – общие уравнения прямой:

Точку М0 находят так: задают произвольно значение z = z0 и из системы находят x = x0, y = y0. Направляющий вектор  параллелен линии пересечения плоскостей и, следовательно, перпендикулярен векторам
параллелен линии пересечения плоскостей и, следовательно, перпендикулярен векторам 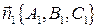 и
и 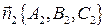 - векторы нормали к плоскостям
- векторы нормали к плоскостям  и
и  . Поэтому в качестве
. Поэтому в качестве  можно взять вектор
можно взять вектор 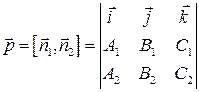 .
.
Следовательно,  имеет следующие координаты:
имеет следующие координаты:

и канонические уравнения прямой имеют вид:
 .
.
Дата добавления: 2014-12-30; просмотров: 715; Мы поможем в написании вашей работы!; Нарушение авторских прав |
