
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
IV. Задачи для самостоятельной работы. 1. Установить взаимное расположение следующих пар плоскостей:
1. Установить взаимное расположение следующих пар плоскостей:
а) 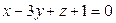 ,
, 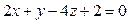 ;
;
б)  ,
, 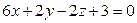 ;
;
в)  ,
,  ;
;
г) 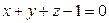 ,
, 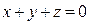 .
.
2. Составить уравнение плоскости, проходящей через начало координат и параллельной плоскости: а)  ; б)
; б)  ; в)
; в) 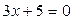 .
.
3. Составить уравнение плоскости, проходящей через точку А(1;–1;2) и параллельной плоскости: а) 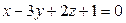 ; б)
; б) 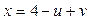 ,
,  ,
,  .
.
4. Даны две плоскости. Установить, являются ли они пересекающимися, параллельными или совпадающими:
а)  и
и 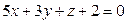 ;
;
б)  и
и  ;
;
в)  ,
, 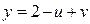 ,
,  и
и  ,
,  ,
, 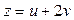 .
.
5. При каких a плоскости  и
и  : 1) пересекаются; 2) параллельны; 3) совпадают?
: 1) пересекаются; 2) параллельны; 3) совпадают?
6. Определить, при каких значениях  и
и  следующие пары уравнений будут определять параллельные плоскости:
следующие пары уравнений будут определять параллельные плоскости:
1) 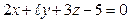 ,
,  ;
;
2)  ,
,  ;
;
3)  ,
,  .
.
7. Определить, при каком значении 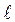 следующие пары уравнений будут определять перпендикулярные плоскости:
следующие пары уравнений будут определять перпендикулярные плоскости:
1) 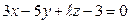 ,
,  ;
;
2) 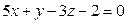 ,
,  ;
;
3)  ,
, 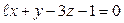 .
.
8. Найти угол между плоскостями:
а) 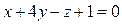 и
и  ;
;
б)  и
и  ;
;
в)  и
и  ;
;
г) 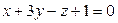 и
и 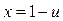 ,
, 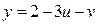 ,
,  ;
;
д) 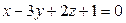 и
и  .
.
9. Составить уравнение плоскости1, проходящей через точку А(2;1;–1) и перпендикулярной двум плоскостям: 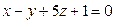 и
и 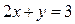 .
.
10. В пучке, определяемом плоскостями 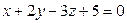 и
и  , найти две перпендикулярные друг другу плоскости, одна из которых проходит через точку М(1;3;1).
, найти две перпендикулярные друг другу плоскости, одна из которых проходит через точку М(1;3;1).
11. Показать, что плоскости  ,
,  и
и  пересекаются в одной точке; найти ее координаты.
пересекаются в одной точке; найти ее координаты.
12. Показать, что плоскости  ,
, 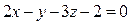 и
и  пересекаются по одной прямой.
пересекаются по одной прямой.
13. Показать, что плоскости 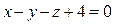 ,
, 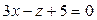 ,
, 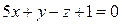 пересекаются по трем параллельным между собой прямым.
пересекаются по трем параллельным между собой прямым.
14. Найдите угол между плоскостями, проходящими через точку М(1;–1;–1), одна из которых содержит ось Ox, а другая – ось Oz.
15. Напишите уравнение плоскости, проходящей через точки М(2;0;0) и Р(0;2;0) и образующей угол 450 с плоскостью 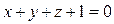 .
.
16. Через линию пересечения плоскостей 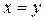 и
и  проведите плоскость под углом 450 к плоскости XOY.
проведите плоскость под углом 450 к плоскости XOY.
17. Написать уравнение плоскости, перпендикулярной плоскости  и пересекающей ее по прямой, лежащей в плоскости OYZ.
и пересекающей ее по прямой, лежащей в плоскости OYZ.
18. В прямоугольной декартовой системе координат даны уравнения граней трехгранного угла
 ,
,
 ,
,
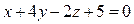 .
.
Написать уравнения трех плоскостей, каждая из которых проходит через некоторое ребро и перпендикулярна противолежащей грани.
19.Определить двугранные углы между следующими парами плоскостей:
а)  ,
,  ;
;
б) 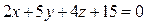 ,
,  .
.
Занятие № 7.
Тема: Расстояние от точки до плоскости.
Геометрический смысл знака многочлена 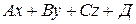 .
.
Дата добавления: 2014-12-30; просмотров: 569; Мы поможем в написании вашей работы!; Нарушение авторских прав |