IV. Задачи для самостоятельной работы.

1. Напишите уравнение плоскости, проходящей через:

а) точку М(–3;2;–5) параллельно плоскости XOY;

б) точки М₁(1;2;3) и Р(2;3;1) параллельно оси аппликат;

в) точку М(4;5;–5) и ось абсцисс;

г) начало координат параллельно векторам и .

2. Составить уравнение плоскости, которая проходит через точку М₁(2;1;–1) и имеет нормальный вектор .

3. Составить уравнение плоскости, проходящей через три точк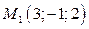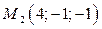и: , и .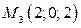

4. Составить уравнение плоскости, которая проходит через начало координат перпендикулярно к двум плоскостям: , .

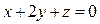5. Составить уравнение плоскости, которая проходит через две точк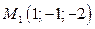и и 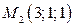перпендикулярно к плоскости .

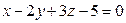6. Плоскость проходит через точку М₁(6;–10;1) и отсекает на оси абсцисс отрезок а = –3 и на оси аппликат отрезок с = 2. Составить для этой плоскости уравнение «в отрезках».

7. Составить уравнение плоскости, отсекающей на оси Oz отрезок с = –5 и перпендикулярной к вектору .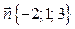

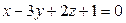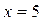8. Составить уравнение плоскости, проходящей через точку А(1;–1;2) и параллельной плоскости: а) ; б) ; в) , , .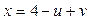

9. Три грани параллелепипеда лежат в плоскостях 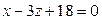, , , 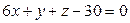а одна из его вершин А имеет координаты (–1;3;1). Составить уравнение остальных граней параллелепипеда.

10. Точки А(1;0;3) и В(–1;2;1) являются вершинами тетраэдра АВСД, точка К(–1;5;2) – серединой ребра ВС, а точка М(0;1;4) – точкой пересечения медиан грани ВСД. Составить уравнения плоскостей, в которых лежат грани тетраэдра.

Занятие № 6.

Тема: Взаимное расположение плоскостей. Пучок плоскостей. Угол между плоскостями.