I. Теоретические сведения. Направляющими векторами плоскости называются два неколлинеарных вектора и , параллельных плоскости.

Направляющими векторами плоскости называются два неколлинеарных вектора 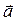и 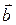, параллельных плоскости.

Любой ненулевой вектор, перпендикулярный плоскости, называется вектором нормали плоскости.

Основные виды уравнений плоскости

1. Векторное уравнение плоскости, заданной точкой М₀ и направляющими векторам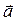и и .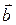

< > - параметры.

2. Параметрические уравнения плоскости, заданной точкой М₀(х₀,у₀,z₀)_R и направляющими векторами и

3. Каноническое уравнение плоскости, заданной точкой М₀(х₀,у₀,z₀)_R и направляющими векторами и

4. Уравнение плоскости, заданной тремя точками, не лежащими на одной прямой М₁(x₁,y₁,z₁), M₂(x₂,y₂,z₂), M₃(x₃,y₃,z₃)_R

5. Уравнение плоскости, заданной двумя точками М₁(x₁;y₁;z₁), M₂(x₂;y₂;z₂) и параллельным плоскости вектором , где 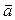не параллелен .

6. Уравнение плоскости «в отрезках».

7. Уравнение плоскости в прямоугольной декартовой системе координат.

8. Общее уравнение плоскости

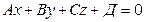, где

Геометрический смысл коэффициентов А, В, С в прямоугольной декартовой системе координат состоит в том, что перпендикулярен плоскости.

Теорема. Любая плоскость в пространстве имеет уравнение вида , где А, В, С – действительные числа, не равные нулю одновременно, т.е. . Справедливо и обратное утверждение: любое уравнение первой степени вида 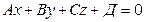определяет плоскость в пространстве.