КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
I. Теоретические сведения. Смешанным произведением трех некомпланарных векторов , и , взятых в определенном порядке, называется скалярное произведение вектора
Смешанным произведением трех некомпланарных векторов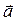 
, 
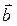и 
, взятых в определенном порядке, называется скалярное произведение вектора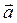 
на векторное произведение векторов 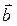и 
.
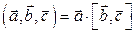
Геометрический смысл смешанного произведения векторов заключается в том, что оно с точностью до знака совпадает с объемом
параллелепипеда, построенного на векторах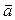 
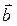, и как на сторонах.
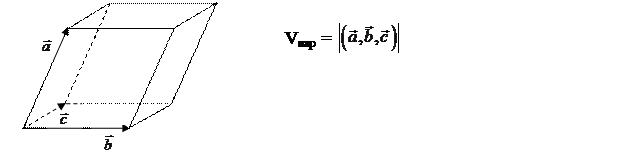
Свойства смешанного произведения
Пусть в Е3 задан правый ортонормированный репер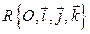 
1. Смешанное произведение векторов, заданных своими координатами численно равно определителю третьего порядка, составленного из координат векторов.
Пусть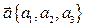 
, 
, 
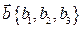, тогда
.
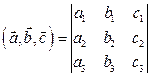Если базис левый, то знак смешанного произведения меняется на противоположный.
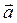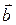2. Тройка некомпланарных векторов , 
, одинаково ориентирована с тройкой базисных векторов 
, 
, 
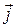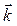тогда и только тогда, когда 
>0.
3. Три вектора компланарны тогда и только тогда, когда смешанное произведение этих векторов равно нулю.
4. Смешанное произведение не меняет значения при циклической перестановке векторов, и меняет знак при перестановке двух векторов.
; 
…
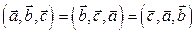
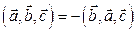5. Операция смешанного произведения векторов линейна по каждому аргументу.
а)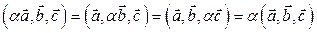 
б) 
6. 
Дата добавления: 2014-12-30; просмотров: 141; Мы поможем в написании вашей работы!; Нарушение авторских прав |