IV. Задачи для самостоятельной работы. 1. Найти смешанное произведение векторов и определить ориентацию тройки векторов в каждом из следующих случаев: а)

1. Найти смешанное произведение векторов и определить ориентацию тройки векторов в каждом из следующих случаев: а) , , ; б) .

2. Определить, какой является тройка (правой или левой), если:

1) ; 2) .

3. Даны три некомпланарных вектора , , . Компланарны ли векторы , и ?

4. Векторы некомпланарны. При каких значениях скаляра компланарны векторы , , ?

5. Даны точки А(2;1;-1), В(3;0;2), С(5;1;1), Д(0;-1;3), являющиеся вершинами тетраэдра. Найти: 1) объем тетраэдра; 2) длину высоты тетраэдра, опущенной из вершины С.

6. Пусть и - произвольные векторы. Проверить тождества:

а) ;

б) ;

в) .

7. Объем тетраэдра V = 5, три его вершины находятся в точках А(2;1;–1), В(3;0;1), С(2;–1;3). Найти координаты четвертой вершины Д, если известно, что она лежит на оси Oy.

8. Дан параллелепипед АВСДА'В'С'Д', построенный на векторах , и . Найти: а) объем параллелепипеда; б) площади граней; в) длину высоты, проведенной из вершины А' на грань АВСД; г) косинус угла между ребром АВ и диагональю В'Д; д) косинус угла между гранями АВСД и АД Д' А'.

9. В треугольной призме АВС А'В'С' векторы , определяют основание, а вектор направлен по боковому ребру. Найти: а) объем призмы; б) площади граней; в) высоту; г) угол 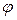между ребрами В'С' и А А'.

10. Дан тетраэдр, построенный на векторах , и . Найти: а) объем тетраэдра; б) площади граней; в) длину высоты h, проведенной из вершины Д; г) косинус угла между ребрами АВ и ВС; д) косинус угла между гранями АВС и АДС.

Занятие № 5.

Тема: Различные способы задания плоскости в пространстве.