КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
I. Теоретические сведения. Возможны следующие случаи взаимного расположения двух плоскостей в пространстве:
Возможны следующие случаи взаимного расположения двух плоскостей в пространстве:
1. Плоскости 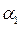 и
и  пересекаются по прямой d
пересекаются по прямой d 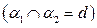 ;
;
2. Плоскости 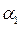 и
и 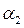 параллельны
параллельны 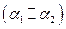 ;
;
3. Плоскости 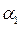 и
и  совпадают
совпадают 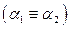 .
.
Пусть относительно некоторой прямоугольно декартовой системы координат  плоскости заданы общими уравнениями:
плоскости заданы общими уравнениями:

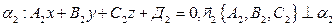
Пусть  ,
,  , тогда справедливы следующие утверждения:
, тогда справедливы следующие утверждения:
1. 
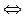 r = 2
r = 2
2. 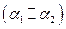
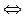 r = 1, r' = 2
r = 1, r' = 2
3. 
 r = 1, r' = 1.
r = 1, r' = 1.
Пусть даны две пересекающиеся плоскости 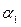 и
и  :
:
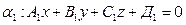 ;
;
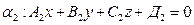 .
.
Углом 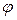 между плоскостями называется любой из двугранных углов, образованных этими плоскостями. Угол
между плоскостями называется любой из двугранных углов, образованных этими плоскостями. Угол 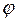 между пересекающимися плоскостями
между пересекающимися плоскостями 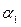 и
и  вычисляется по формуле:
вычисляется по формуле:
 .
.
Отсюда следует, что плоскости 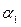 и
и  перпендикулярны тогда и только тогда, когда
перпендикулярны тогда и только тогда, когда 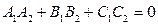 .
.
Пучком плоскостей называется совокупность плоскостей, проходящих через одну прямую.
|

Тогда уравнение  , где
, где 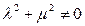 называется уравнением пучка плоскостей.
называется уравнением пучка плоскостей.
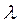 и
и 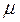 не равны нулю одновременно
не равны нулю одновременно 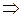 обозначим
обозначим 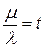 , где
, где 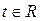 и уравнение пучка плоскостей можно записать в виде:
и уравнение пучка плоскостей можно записать в виде:
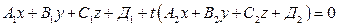 .
.
Дата добавления: 2014-12-30; просмотров: 633; Мы поможем в написании вашей работы!; Нарушение авторских прав |
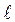 - ось пучка.
Пусть плоскости
- ось пучка.
Пусть плоскости 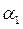 и
и  ;
;