
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
V. Задачи для самостоятельного решения. 1. Привести к нормальному виду уравнения плоскостей: а) ; б) ; в) ; г)
1. Привести к нормальному виду уравнения плоскостей: а)  ; б)
; б)  ; в)
; в)  ; г)
; г) 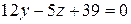 ; д)
; д)  ; е)
; е)  .
.
2. Для каждой из следующих плоскостей вычислить углы  ,
,  и
и  , образуемые нормалью с осями координат, и расстояние p от начала координат: а)
, образуемые нормалью с осями координат, и расстояние p от начала координат: а)  ; б)
; б)  ; в)
; в) 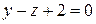 ; г)
; г)  ; д)
; д)  ; е)
; е) 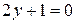 .
.
3. Вычислить расстояние d от точки Р(–1;1;–2) до плоскости, проходящей через три точки М1(1;–1;1), М2(–2;1;3) и М3(4;–5;–2).
4. Найти расстояние от точки М(2;–1;–1) до плоскости  .
.
5. На оси Oz найти точку, расстояние которой от плоскости  равно 2.
равно 2.
6. На оси Oy найти точку, равноудаленную от точки А(0;2;1) и от плоскости  .
.
7. На оси Ox найти точку, равноудаленную от двух плоскостей:  ,
, 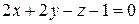 .
.
8. На оси Oz найти точку, равноудаленную от точки М(1;–2;0) и от плоскости  .
.
9. Две грани куба лежат на плоскостях  ,
,  . Вычислить объем этого куба.
. Вычислить объем этого куба.
10. Составить уравнения плоскостей, параллельных плоскости  и отстоящих от нее на расстоянии d = 5.
и отстоящих от нее на расстоянии d = 5.
11. Составить уравнение множества точек, отстоящих от плоскости 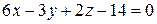 на расстоянии, равном 3.
на расстоянии, равном 3.
12. Найти уравнение плоскости, касающейся сферы  и параллельной плоскости
и параллельной плоскости 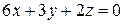 .
.
13. У треугольной пирамиды SABC вершина S совпадает с началом координат, а боковые грани – с координатными плоскостями. Написать уравнение плоскости основания ABC, если SA:SB:SC = 1:3:2, а высота SH = 6, и вершины A, B и С имеют неотрицательные координаты.
14. В каждом из следующих случаев определить, лежат ли точка М(2;–1;3) и начало координат в одном, в смежных или вертикальных двугранных углах, образованных при пересечении двух плоскостей:
а)  , б)
, б)  ,
,
 ;
; 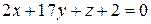 .
.
15. Составить уравнение плоскости, которая делит пополам острый двугранный угол, образованный двумя плоскостями: 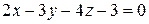 ,
,  .
.
16. Составить уравнение плоскости, делящей пополам тот двугранный угол между двумя плоскостями  ,
,  , в котором лежит начало координат.
, в котором лежит начало координат.
17. Доказать, что плоскость  пересекает отрезок, ограниченный точками М1(3;–2;1) и М2(–2;5;2), и не пересекает отрезок, ограниченный точками N1(1;4;–3) и N2(2;5;0).
пересекает отрезок, ограниченный точками М1(3;–2;1) и М2(–2;5;2), и не пересекает отрезок, ограниченный точками N1(1;4;–3) и N2(2;5;0).
Дата добавления: 2014-12-30; просмотров: 423; Мы поможем в написании вашей работы!; Нарушение авторских прав |