
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
V. Задачи для самостоятельной работы. 1. Доказать, что: а) прямая пересекает ось Oy;
1. Доказать, что: а) прямая  пересекает ось Oy;
пересекает ось Oy;
б) прямая  пересекает координатные плоскости. Определить координаты точек пересечения.
пересекает координатные плоскости. Определить координаты точек пересечения.
2. Установить взаимное расположение следующих пар прямых: а)  и
и 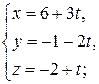 б)
б) 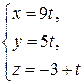 и
и  в)
в)  и
и  ; г)
; г)  и
и 
3. Доказать, что прямые  и
и  пересекаются. Написать уравнение плоскости, проходящей через эти прямые.
пересекаются. Написать уравнение плоскости, проходящей через эти прямые.
4. Доказать, что следующие пары прямых параллельны: а)  ,
, 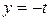 ,
,  и
и  б)
б) 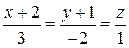 и
и  Составить уравнения плоскостей, проходящих через каждую пару прямых.
Составить уравнения плоскостей, проходящих через каждую пару прямых.
5. Доказать, что прямые взаимно перпендикулярны:
а)  и
и  б)
б)  и
и  в)
в)  и
и 
6. Найти угол между прямыми: а)  и
и  ; б)
; б)  и
и  в)
в)  и
и 
7. Вычислить углы, образованные противоположными ребрами тетраэдра с вершинами: A(3;–1;0), B(0;–7;3), C(–2;1;–1), Д(3;2;6).
8. Через точку (2;–5;3) провести прямую:
1) параллельную оси Oz;
2) параллельную прямой  ;
;
3) параллельную прямой 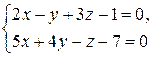 .
.
9. Составить уравнения прямой, проходящей через точку М(3;–2;0) перпендикулярно к прямой 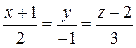 и расположенной в плоскости XOY.
и расположенной в плоскости XOY.
10. Составить уравнения прямой, проходящей через точку N(1;2;–1) параллельно линии пересечения плоскостей 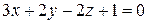 и
и 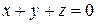 .
.
11. Доказать, что следующие прямые  и
и 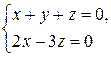 скрещиваются.
скрещиваются.
12. Доказать, что прямые  и
и  пересекаются и найти их точку пересечения.
пересекаются и найти их точку пересечения.
13. Даны прямые  ,
,  ; при каком значении
; при каком значении  они пересекаются?
они пересекаются?
Занятие № 10.
Тема: Поверхности вращения.
Цилиндрические поверхности
Дата добавления: 2014-12-30; просмотров: 445; Мы поможем в написании вашей работы!; Нарушение авторских прав |