I. Теоретические сведения. Пусть в пространстве дана некоторая плоская линия g и точка S, не лежащая в плоскости этой линии.

Пусть в пространстве дана некоторая плоская линия g и точка S, не лежащая в плоскости этой линии.

Определение. Конической поверхностью называется множество точек пространства, лежащих на прямых проходящих через данную точку S и пересекающих данную линию g.

Линия g называется направляющей конической поверхности, точка S – вершиной, прямые называются образующими.

Рассмотрим частный случай: вершина S совпадает с началом координат, направляющая линия g лежит в плоскости, параллельной плоскости xOy: z=c, и задается уравнением: .

В этом случае уравнение конической поверхности имеет вид

. (1)

Если направляющая является эллипсом с центром на оси Oz,

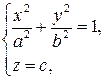
то получаем поверхность, называемую конусом второго порядка, уравнение этой поверхности имеет вид:

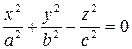. (2)

Ось Oz в этом случае является осью конуса второго порядка.

Сечения конуса второго порядка:

Пусть плоскость p не проходит через вершину конуса второго порядка, тогда плоскость p пересекает конус:

а) по эллипсу, если p пересекает все образующие конуса;

б) по гиперболе, если p параллельна двум образующим конуса;

в) по параболе, если p параллельна одной образующей конуса.