IV. Примеры решения задач. Задача 1. Найти фигуру, состоящую из всех точек, одинаково удаленных от данной плоскости a и данной точки А

Задача 1. Найти фигуру, состоящую из всех точек, одинаково удаленных от данной плоскости a и данной точки А, не лежащей в этой плоскости.

Решение.

Обозначим расстояние между точкой А и плоскостью a через р. Введем в пространстве систему координат так, чтобы начало координат находилось посередине между точкой А и плоскостью a, плоскость xOy была параллельна плоскости a. Тогда точка А имеет координаты , а уравнение плоскости a имеет вид . Пусть точка произвольная точка, удовлетворяющая условию задачи. Тогда

,

.

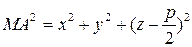По условию , следовательно, , т.е.

,

,

,

.

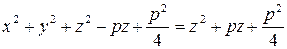Таким образом, искомое множество точек есть эллиптический параболоид, заданный последним уравнением.

Ответ: .

Задача 2. Исследовать методом сечений поверхность .

Решение.

Исследуем сечения гиперболического параболоида координатными плоскостями и плоскостями им параллельными.

1) Сечение плоскостью a, параллельной плоскости .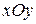

Или

.

а) Если , то линия пересечения гипербола с действительной осью параллельной оси Ох;

б) если , то линия пересечения гипербола с действительной осью параллельной оси Oy;

в) если , то линия пересечения пара действительных пересекающихся прямых.

2) Сечение плоскостью b, параллельной плоскости .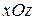

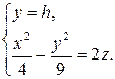
Или

.

При любом значении h получаем параболу, ось которой параллельна оси Oz, В частности, если , то 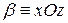, и в сечении мы получаем параболу ;

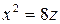3) Сечение плоскостью g, параллельной плоскости .

Или

.

При любом значении h получаем параболу, ось которой параллельна оси Oz, ветви направлены вниз. В частности, если , то , и в сечении мы получаем параболу .

Задача 3. Написать уравнения двух систем прямолинейных образующих однополостного гиперболоида и определить те из них, которые проходят через точку .

Решение.

Приведем уравнение гиперболоида к каноническому виду:

.

Перенесем второе слагаемое в правую часть

.

Применим формулу разности квадратов

.

Равенство имеет место в том случае, если множители в левой и правой частях пропорциональны

I. II.

Мы получили уравнения двух систем прямолинейных образующих однополостного гиперболоида. Теперь найдем те из них, которые проходят через данную точку . Подставим координаты точки в каждую из систем:

I.

Откуда получаем

.

Подставляя это соотношение в систему I, получаем

– общие уравнения прямолинейной образующей.

I.

Откуда получаем

.

Подставляем в II:

– общие уравнения прямолинейной образующей.

Ответ: и