помощью действительных чисел, где называется тригонометрическим рядом, а числа его коэффициентами.

14.Ряд Фур’є для парних і непарних функцій. Дискретний спектр функції. Ряд Фур’є в комплексній формі. Комплексний дискретний спектр функції.

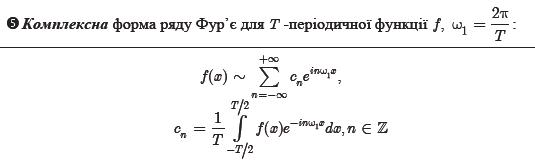
15.Інтеграл Фур’є ,(простий та подвійний). Теорема про збіжність Інтегралу Фур’є. Інтеграл Фур’є парних і непарних функцій. Синус і косинус перетворення Фур’є. Спектр функції.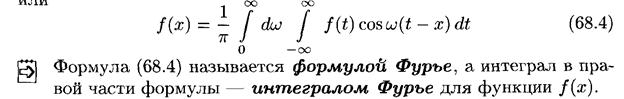

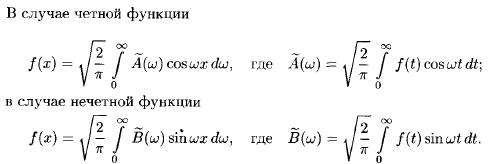
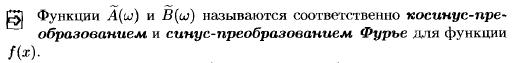
17. Похідна ФКЗ: означення. Умови Коші-Рімана. Приклад.

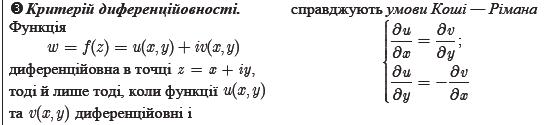
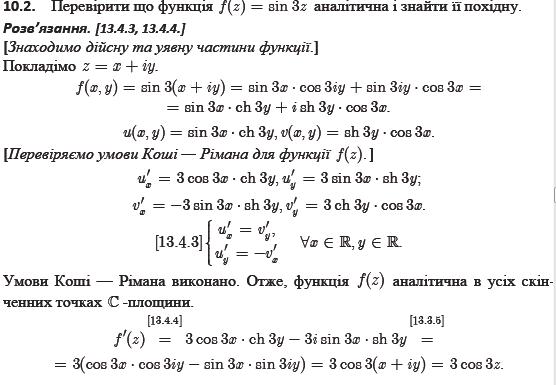
18. Означення аналітичної функції в точці та на множині. Приклад. Гармонічні функції та їх зв’язок з аналітичними. Відновлення аналітичної функції по її дійсній частині.

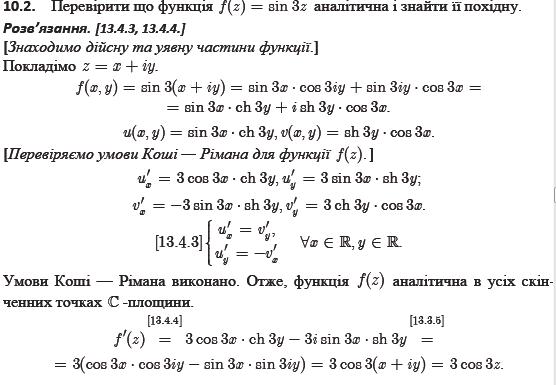
19. Означення інтеграла в комплексній області та його обчислення. Властивості цього інтеграла (довести теорему про оцінку модуля).

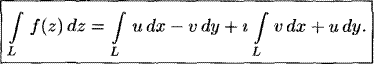
20.Інтегральна теорема Коші. Наслідок для неоднозв’язних областей та системи контурів. Обчислення інтеграла ∮ , де n-ціле число , Г-довільний контур.

21.Первісна аналітичної функції. Теорема існування та формула Ньютона-Лейбніца.

22.Інтегральна формула Коші. Інтеграл типу Коші та його аналітичність.

23. Теорема про перехід до границі під знаком інтеграла. Теорема Вейерштрасса про послідовності аналітичних функцій. Наслідок для рядів.