Тест тапсырмасы

«Экономикадағы математика» (3 кредит) пәнінен

1 курс, 5В050600– Экономика, 5В050700–Менеджмент, 5В050800– Учет иаудит, 5В050900– Финансы, 5В051000– ГМУ мамандықтарының студенттері үшін

1. Квадраттық матрица диагональдық деп аталады, егер

A) бас диагональдан басқа элементтері нөлге тең болса

B) жанама диагональ элементтері нөлге тең

С) бас диагональ элементтері нөлге тең

D) матрицаның барлық элементтері нөлге тең

E) бас диагональдан басқа элементтері бірге тең болса

2. өлшемді тікбұрышты матрицасы квадраттық деп аталады, егер …

A)

B)

С)

D)

E)

3. Матрицаны санға көбейткенде .......... көбейтіледі

A) матрицаның барлық элементі сол санға

B) қандайда бір бағанның барлық элементіне

С) қандайда бір жолдың барлық элементіне

D) жанама диагональдің барлық элементіне

E) бас диагональдің барлық элементіне

4. Екі матрицаны тек сонда ғана көбейтуге болады, егер :

А) бірінші матрицаның бағандарының саны екінші матрицаның жолдарының санына тең болса

В) бірінші матрицаның жолдарының саны екінші матрицаның бағандарының санына тең болса

С) бірінші матрицаның бағандарының саны екінші матрицаның бағандарының санына тең болса

D) екі матрицаның да жолдары мен бағандарының саны сәйкесінше тең болса

E) бірінші матрицаның жолдарының саны екінші матрицаның жолдарының санына тең болса

5. Екі матрицаны қосуға болады, егер...

А) екі матрицаның да жолдары мен бағандарының саны сәйкесінше тең болса

В) бірінші матрицаның жолдарының саны екінші матрицаның бағандарының санына тең болса

С) бірінші матрицаның бағандарының саны екінші матрицаның бағандарының санына тең болса

D) бірінші матрицаның бағандарының саны екінші матрицаның жолдарының санына тең болса

E) бірінші матрицаның жолдарының саны екінші матрицаның жолдарының санына тең болса

6. Анықтауыштың шамасы нөлге тең, егер :

А) екі жолдың (бағанның) сәйкес элементтері пропорционал болса

В) қандайда бір жолдың (бағанның) барлық элементтері нөлге тең емес санға көбейтілсе

С) анықтауыштың кез келген екі жолын (бағанын) алмастырса

D) анықтауыштың жолдарын бағандармен алмастырса

E) қандайда бір жол (баған) элементтерінің ортақ көбейткішін анықтауыш белгісінің алдына шығарса

7. Анықтауыштың шамасы өзгермейді, егер :

А) қандайда бір жол (баған) элементтерінің ортақ көбейткішін анықтауыш белгісінің алдына шығарса

В) қандайда бір жолдың (бағанның) барлық элементтері нөлге тең емес санға көбейтілсе

С) анықтауыштың кез келген екі жолын (бағанын) алмастырса

D) қандайда бір жол (баған) элементтерінің көбейткішін анықтауыш белгісінің алдына шығарса

E) бас (жанама)диагональ элементтерінің ортақ көбейткішін анықтауыш белгісінің алдына шығарса

8. элементінің алгебралық толықтауышы мен миноры арасындағы байланыс:

А)

В)

С)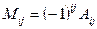

D)

E)

9. Екінші ретті квадраттық матрицаның анықтауышын есептеу формуласы:

А)

В)

C)

D)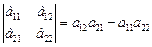

E)

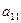10. анықтауышындағы элементінің минорын табу керек:

A)

B)

C)

D)

Е)

11. Теңдеуді шешу керек :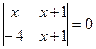

A)

B)

C)

D)

E)

12. Үшінші ретті квадраттық матрицаның анықтауышын есептеу керек :

А)

В)

С)

D)

E)

13. Үшінші ретті квадраттық матрицаның анықтауышын есептеу керек :

A)

В)

С)

D)

E)

14. 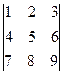анықтауышындағы элементінің минорын табу керек:

A)

B)

C)

D)

E)

15. анықтауышындағы элементінің алгебралық толықтауышын табу керек:

A)

B)

C)

D)

E)

16. болсын. 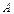матрицасының анықтауышын есептеу керек:

A)

B)

C)

D)

E)

17. матрицасын табу керек, егер :

А)

В)

С)

D)

Е)

18. 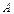және матрицаларының көбейтіндісін табу керек, егер , :

A) көбейтуге болмайды

B)

C)

D)

E)

19. және матрицаларының көбейтіндісі мүмкін болса, онда :

A)

B) көбейту мүмкін емес

C)

D)

E)

20. 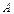және матрицаларының көбейтіндісін табу керек, егер , :

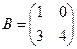A)

B)

C)

D)

E)

21. 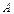квадраттық матрицасы ерекшеленген емес деп аталады, егер :

А)

В)

С)

D)

Е)

22. Екінші ретті 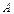квадраттық матрицасы үшін 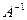кері матрицаны табу формуласы :

A)

B)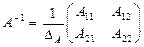

C)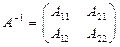

D)

Е)

23. кері матрицасын табу керек, егер :

А)

В)

С)

D)

Е)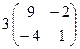

24. Екінші ретті квадраттық матрица үшін табу керек :

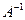A)

B)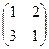

C)

D)

E)

25. Үшінші ретті 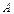квадраттық матрицасы үшін кері матрицаны табу формуласы.

A)

B)

C)

D)

Е)

26. Сызықты алгебралық теңдеулер жүйесі үйлесімді деп аталады, егер:

А) ең болмағанда бір шешімі болса

B) шексіз көп шешімі болса

C) шешімдерінің саны белгісіздер санына тең болса

D) шешімдерінің саны теңдеулер санына тең болса

Е) жалғыз шешімі болса

27. Үйлесімді сызықты алгебралық теңдеулер жүйесінің жалғыз шешімі болса. онда …… деп аталады.

А) Анықталған

B) Үйлесімсіз

C) Біртекті

D) Біртекті емес

Е) Эквивалентті

28. Сызықты алгебралық теңдеулер жүйесінің әр уақытта шешімі болады, егер ...

А) жүйенің анықтауышы нөлден өзгеше болса

B) жүйенің анықтауышы нөлге тең болса

C) жүйенің анықтауышы теріс таңбалы болса

D) жүйенің анықтауышы бірге тең болса

Е) жүйе матрицасының рангісі үшке тең болса

29. үш белгісізі бар үш теңдеуден тұратын САТЖ –нің шешімдерін табудың Крамер формулалары :

А)

В)

С)

D)

E)

30. 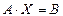матрицалық теңдеуінің шешімін табу формуласы, мұндағы :

A)

B)

С)

D)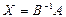

E)

31. Сызықты алгебралық теңдеулер жүйесінде элементар түрлендірулер қандай жағдайда қолданылады?

А) САТЖ-ін Гаусс әдісімен шешуде

В) САТЖ-ін Крамер формуласымен шешуде

С) САТЖ-ін матрицалық әдіспен шешуде

D) САТЖ-інің матрицасының анықтауышын есептеуде

Е) САТЖ-інің матрицасының рангісін табуда

32. САТЖ-і берілген . Жүйеден -тің мәнін табу керек :

A)

B)

C)

D)

E)

33. САТЖ-ін шешіп, -тің мәнін табу керек :

A)

B)

C)

D)

E)

34. САТЖ-ін шешіп , -тің мәнін табу керек :

A)

B)

C) .

D)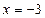

E)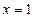

35. САТЖ-ін шешіп , -дің мәнін табу керек :

A)

B)

C)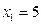

D)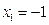

E)

36. САТЖ-ін шешу керек :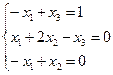

A)

B)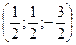

C)

D)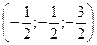

E)

37. САТЖ-ін шешіп , -нің мәнін табу керек :

A)

B)

C)

D)

E)

38. САТЖ-ін шешіп , 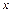-тің мәнін табу керек :

A)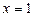

B)

C)

D)

E)

39. САТЖ берілген . Табу керек

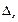
А)

B)

C)

D)

Е)

40. Матрицаның k –жолы мен k-бағанының қиылысындағы элементтерден құралған анықтауыш ......... деп аталады.

А) матрицаның k-ретті миноры

В) матрицаның анықтауышы

С) матрицаның базистік миноры

D) матрица элементінің алгебралық толықтауышы

Е) матрица элементінің миноры

41. Матрицаның рангісі деп ….. айтамыз.

А) матрица минорының нөлге тең емес ең үлкен ретін

В) матрица минорының нөлге тең емес ең үлкен шамасын

С) матрицаның базистік минорының ретін

D) матрица минорының ең үлкен ретінің санын

Е) матрица минорының барлық санын

42. Матрицаның рангісі өзгермейді, егер :

А) матрица жолының (бағанының) элементтерін нөлден өзгеше санға көбейтсе

В) матрица жолының (бағанының) қандай да бір элементін нөлден өзгеше санға көбейтсе

С) кейбір элементтері нөлге тең болатын жолды (бағанды) алып тастаса

D) матрица жолының (бағанының) қандай да бір элементінің көбейткішін матрица белгісінің алдына шығарса

E) матрицаның бас диагоналінің элементтерін нөлден өзгеше санға көбейтсе

43. Матрицалар эквивалентті деп аталады, егер:

А) матрица рангілері тең болса

В) осы матрицалардан алынған анықтауыштар тең болса

С) матрицалардың өлшемдері тең болса

D) матрица рангілері тең емес болса

Е) матрицалардың өлшемдері әртүрлі болса

44. Біртекті емес сызықты алгебралық теңдеулер жүйесі үйлесімділігінің қажетті және жеткілікті шарты:

А)

B)

C)

D)

Е)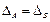

45. Біртекті емес алгебралық теңдеулер жүйесінің жалғыз шешімі болады, егер:

А)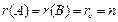

B)

C)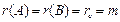

D)

Е)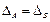

46. Біртекті емес алгебралық теңдеулер жүйесінің шексіз көп шешімі болады, егер:

А)

B)

C)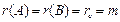

D)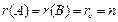

Е)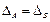

47. Біртекті емес алгебралық теңдеулер жүйесінің үйлесімсіз болады, егер:

А)

B)

C)

D)

Е)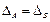

48. Алгебралық теңдеулер жүйесінің бос мүшелері нөлге тең болса, онда :

А) Біртекті деп аталады

B) Үйлесімсіз

C) Анықталған деп аталады

D) Біртекті емес

Е) Эквивалентті

49. Біртекті сызықты алгебралық теңдеулер жүйесінің тривиальді емес шешімі болады, егер:

А)

B)

C)

D)

Е)

50. Матрица рангісін табу керек .

А)

B)

C)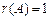

D)

Е)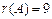

51. Матрица рангісін табу керек .

А)

B)

C)

D)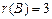

Е)

52. Матрица рангісін табу керек .

А)

B)

C)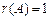

D)

Е)

53. Жүйенің кеңейтілген матрицасының рангісін табу керек .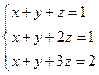

А)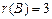

B)

C)

D)

Е)

54. Жүйенің матрицасының рангісін табу керек .

А)

B)

C)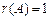

D)

Е)

55. Жүйенің матрицасының базистік минорының ретін табыңыз .

А)

B) Жүйенің матрицасының базистік миноры жоқ

C)

D)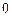

Е)

56. Біртекті жүйе матрицасының базистік минорының ретін табыңыз .

А)

B) 4

C)

D) Жүйенің матрицасының базистік миноры жоқ

Е)

57. Біртекті жүйе матрицасының рангісін табыңыз .

А)

B)

C)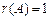

D)

Е)

58. Жүйе матрицасының және кеңейтілген матрицаның рангісін табу керек .

А) ,

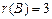
B)

C)

D) ,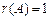

Е) ,

59. Берілген сызықты алгебралық теңдеулер жүйесі …….. жүйе болып табылады. .

А)үйлесімсіз

B) үйлесімді және анықталған

C) біртекті

D) үйлесімді және анықталмаған

Е) эквивалентті

60. Егер және векторлары коллинеар болса, онда

А)

В)

С)

D)

E)

61. Екі және векторларының ортогональдық шарты:

A)

B)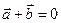

С)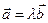

D)

E)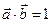

62. Нөлдік емес және векторлары қалай орналасқан, егер :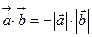

А)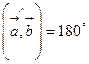

В)

С)

D)

E)

63. Бір түзудің бойында жататын немесе бір түзуге параллель векторлар ..... деп аталады. А) коллинеар

В) нөлдік векторлар

С) сызықты-тәуелсіз

D) қарама-қарсы

E) бірлік

64. Бір жазықтықта орналасқан немесе бір жазықтыққа параллель болатын векторлар .....деп аталады.

А) компланар

В) нөлдік векторлар

С) сызықты-тәуелсіз

D) бірлік

E) коллинеар

65. Кеңістікте векторын базисі бойынша жіктеудің көрінісі:

А)

В)

С)

D)

E)

66. Кеңістіктегі векторының бағыттауыш косинустарын табу формуласы:

А)

В)

С)

D)

Е)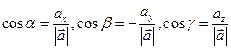

67. және векторларының арасындағы бұрышын анықтау формуласы :

А)

B)

C)

D)

Е)

68. базисі бойынша жіктелген векторы берілген.Осы вектордың аппликатасын көрсетіңіз:

A)

B)

C)

D)

E)

69. векторы үшін бірлік вектордың абсциссасын көрсету керек:

A)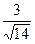

B)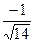

C)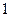

D)

E)

70. векторы берілген. векторы мен осі арасындағы бұрыштың косинусы :

A)

B)

C)

D)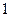

E)

71. 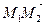векторының координатасын табу керек, егер :

A)

B)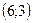

C)

D)

Е)

72. векторының модулін табу керек:

A)

B)

C)

D)

E)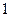

73. бірлік векторының координаталарын көрсетіңіз, егер және нүктелерінің координаталары белгілі болса:

A)

B)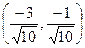

C)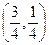

D)

E)

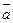74. векторы берілген. векторыныңи 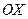осіне проекциясы :

A)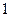

B)

C)

D)

E)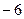

75. векторының екінші координатасын табыңыз,егер және бірінші координатасы 6-ға тең болса:

A)

B)

C)

D)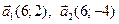

E)

76. векторының және векторлары бойынша жіктелуінің коэффициентін табу керек:

A)

B)

C)

D)

E)

77. 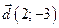векторын және векторлары бойынша жіктеңіз:

A)

B)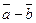

C)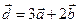

D)

E)

78. , векторлары берілген. коэффициентінің қандай мәнінде 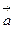және векторлары коллинеар болады:

А)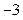

В)

С)

D)

Е)

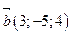79. және векторлары берілген. 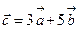векторының координатасын анықтау керек:

А)

В)

С)

D)

Е)

80. векторларының ұзындықтары берілген. Векторлар арасындағы бұрыш 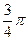. Векторлардың скаляр көбейтіндісін табу керек:

A)

B)

C)

D)

E)

81 векторлары берілген. Ортогональ векторларды көрсетіңіз:

A) и

B) и

C) и

D) Ортогональ векторлар жоқ.

E)

82. Векторлардың векторлық көбейтіндісін табыңыз :

A)

B)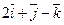

C)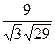

D)

E)

83. Векторлардың аралас көбейтіндісін табу керек :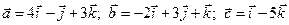

A)

B)

C)

D)

E)

84. векторларының көбейтіндісі:

A)

B)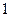

C)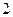

D)

E)

85. векторларының көбейтіндісі :

A)

B)

C)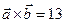

D)

E)

86. векторының координаттарын табыңыз, егер :

A)

B)

C)

D)

Е)

87. векторының координаттарын табыңыз, егер :

A)

B)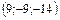

C)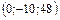

D)

Е)

88. векторының модулін табыңыз , егер :

A)

B)

C)

D)

Е)

89. векторының бағыттауыш косинустарын табыңыз, егер :

А)

В)

С)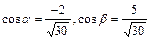

D)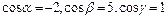

Е)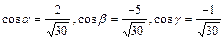

90. векторының базисі бойынша кеңістіктегі жіктелуі , егер :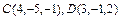

А)

В)

С)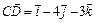

D)

E)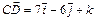

91. 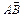және векторларының скаляр көбейтіндісін табыңыз , егер :

A)

B)

C)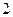

D)

E)

92. шбұрышының ауданын есептеңіз,егер төбелерінің кооординаталары белгілі болса :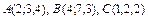

A)

B)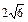

C)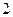

D)

E)

93. және