Вычисление двойного интеграла

Теорема. Если функция f(x, y) непрерывна в замкнутой области D, ограниченной линиями х = a, x = b, (a < b), y = j(x), y = y(x), где j и y - непрерывные функции и

j £ y, тогда

y y = y(x)

D

y = j(x)

a b x Пример. Вычислить интеграл 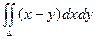, если область D ограничена линиями: y = 0, y = x², x = 2.

y

0 Δ 2 x

=

=

Теорема. Если функция f(x, y) непрерывна в замкнутой области D, ограниченной линиями y = c, y = d (c < d), x = F(y), x = Y(y) (F(y) £ Y(y)), то

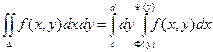
Пример. Вычислить интеграл , если область D ограничена линиями y = x, x = 0, y = 1, y = 2.

y

y = x 2

D

0 x

Пример. Вычислить интеграл , если область интегрирования D ограничена линиями х = 0, х = у², у = 2.

=

=

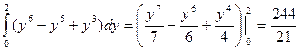
Пример. Вычислить двойной интеграл , если область интегрирования ограничена линиями ху=1, у = , х = 2.

1.

2.

3.

Замена переменных в двойном интеграле

Рассмотрим двойной интеграл вида , где переменная х изменяется в пределах от a до b, а переменная у – от j₁(x) до j₂(х).

Положим х = f(u, v); y = j(u, v)

Тогда dx = ; dy = ;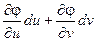

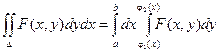
т.к. при первом интегрировании переменная х принимается за постоянную, то dx = 0.

, т.е.

подставляя это выражение в записанное выше соотношение для dy, получаем:

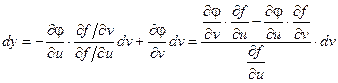
Выражение называется определителем Якобиили Якобианомфункций f(u, v) и j(u, v).

Тогда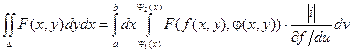

Т.к. при первом интегрировании приведенное выше выражение для dx принимает вид ( при первом интегрировании полагаем v = const, dv = 0), то при изменении порядка интегрирования, получаем соотношение:

Двойной интеграл в полярных координатах

Воспользуемся формулой замены переменных:

При этом известно, что

В этом случае Якобиан имеет вид:

Тогда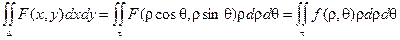

Здесь t - новая область значений,