
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Ранние модели строения атома
Атом (в переводе с греческого – неделимый) долгое время считался простейшей, элементарной частицей мироздания. Но в самом конце XIX века были открыты некоторые явления, а также выполнены эксперименты, результаты которых свидетельствовали о сложности атома:
· Радиоактивность (самопроизвольный распад атомов некоторых элементов);
· Фотоэффект (испускание электронов металлами, при облучении их светом).
· Катодные лучи (испускание потока электронов при создании большой разности потенциалов между двумя металлическими электродами).
Осмысление новых фактов потребовало изменить представление об атоме как о примитивном материальном объекте. Возникла необходимость задуматься об устройстве атома. 
 – После открытия электронов и экспериментального определения их свойств (заряда и массы) в конце XIX – в начале XX веков были предложены несколько моделей строения атомов, в составе которых предполагалось наличие электронов, колеблющихся и или поступательно движущихся в положительно заряженной среде. Таким
– После открытия электронов и экспериментального определения их свойств (заряда и массы) в конце XIX – в начале XX веков были предложены несколько моделей строения атомов, в составе которых предполагалось наличие электронов, колеблющихся и или поступательно движущихся в положительно заряженной среде. Таким
образом, достигалась электронейтральность атома, и качественно объяснялись их спектральные свойства.
– Экспериментальная проверка подобных моделей была выполнена Э.Резерфордом с коллегами. В опытах по рассеянию α-частиц при облучении тонкой золотой фольги было убедительно показано, что в атомах имеется ничтожная по размеру, но очень массивная положительно заряженная частица. Выявленные факты указывали на то, что такая частица в атоме имеется лишь одна. Стало ясно, что отличаются атомы разных элементов величиной положительного заряда этой частицы и числом электронов, суммарный отрицательный заряд которых делает атом нейтральным. Чтобы "предотвратить сближение, прилипание" электронов к положительной частице в предложенной Э.Резерфордом "планетарной" модели строения атома (1911г.) положительная частица размещалась в его центре (ядро атома), а электроны двигались вокруг него по круговым орбитам (как планеты вокруг солнца) под действием центробежной силы.

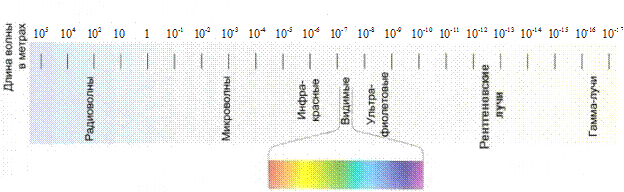
 Модель была проста, основана на узнаваемой аналогии и полностью удовлетворяла выявленным на тот момент сведениям о составе атомов. Но, в то же время, понятная качественная аналогия с солнечной системой таила в себе и серьезную качественную проблему: невозможно представить, чтобы столкновение с другой планетарной системой или телом сопоставимой массы осталось бы без серьезных взаимных последствий, а атомы, сталкиваясь, взаимодействуя друг с другом, не утрачивают своей индивидуальности, могут быть вновь выделены в неизменном виде. Более того, даже в изолированном состоянии атом, устроенный в соответствии с моделью Резерфорда, не мог быть стабилен. Дело в том, что в соответствии с законами классической электродинамики (раздел физики, описывающий законы движения заряженных тел) движущаяся по круговой орбите заряженная частица (электрон) обязан испускать энергию. Но при этом будет нарушаться баланс центробежной силы и силы кулоновского притяжения отрицательного электрона к положительному ядру атома. Поэтому электрон в итоге должен упасть на ядро. В соответствие с выполненными оценочными расчетами, "время жизни" атома в планетарном виде не должно превышать ~10-8с. Непрерывное понижение энергии электрона должно было приводить к "непрерывному", сплошному спектру испускания атома, в котором бы присутствовали компоненты электромагнитного излучения с разными, непрерывно меняющимися длинами волн. На самом деле атомные спектры испускания всегда содержат набор отдельных линий (линейчатый спектр). Причем еще в конце XIXв были установлены важные закономерности в их структурах. Простейшая спектральная картина наблюдалась при термическом возбуждении атомарного водорода (в искровой дуге). В воспринимаемой человеческим глазом части спектра (рис.1.3(а)) наблюда-
Модель была проста, основана на узнаваемой аналогии и полностью удовлетворяла выявленным на тот момент сведениям о составе атомов. Но, в то же время, понятная качественная аналогия с солнечной системой таила в себе и серьезную качественную проблему: невозможно представить, чтобы столкновение с другой планетарной системой или телом сопоставимой массы осталось бы без серьезных взаимных последствий, а атомы, сталкиваясь, взаимодействуя друг с другом, не утрачивают своей индивидуальности, могут быть вновь выделены в неизменном виде. Более того, даже в изолированном состоянии атом, устроенный в соответствии с моделью Резерфорда, не мог быть стабилен. Дело в том, что в соответствии с законами классической электродинамики (раздел физики, описывающий законы движения заряженных тел) движущаяся по круговой орбите заряженная частица (электрон) обязан испускать энергию. Но при этом будет нарушаться баланс центробежной силы и силы кулоновского притяжения отрицательного электрона к положительному ядру атома. Поэтому электрон в итоге должен упасть на ядро. В соответствие с выполненными оценочными расчетами, "время жизни" атома в планетарном виде не должно превышать ~10-8с. Непрерывное понижение энергии электрона должно было приводить к "непрерывному", сплошному спектру испускания атома, в котором бы присутствовали компоненты электромагнитного излучения с разными, непрерывно меняющимися длинами волн. На самом деле атомные спектры испускания всегда содержат набор отдельных линий (линейчатый спектр). Причем еще в конце XIXв были установлены важные закономерности в их структурах. Простейшая спектральная картина наблюдалась при термическом возбуждении атомарного водорода (в искровой дуге). В воспринимаемой человеческим глазом части спектра (рис.1.3(а)) наблюда-
А

Б
| Рисунок 1.3 – Полный энергетический спектр электромагнитного излучения (а) и спектр испускания атома водорода (б) |
ются четыре отдельные линии (рис.1.3(б)). В 1885г. швейцарский физик И.Я.Бальмер эмпирическим путем установил, что длины волн соответствующих линий пропорциональны одному изменяющемуся целому числу:
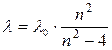 (1.1)
(1.1)
где λ0 – некоторая постоянная длина волны; n принимает целые значения 3, 4, 5 и т.д.
В 1900г. шведский физик И.Р.Ридберг, анализируя спектральные свойства, в том числе, других элементов, показал, что подобные закономерные серии наблюдаются и в спектрах испускания атомов других элементов, причем они все могут быть описаны одной обобщенной формулой:
 = R·(1/n12 – 1/n22) (1.2)
= R·(1/n12 – 1/n22) (1.2)
где константа R = 109 677 см-1 получила в дальнейшем название постоянной Ридберга; n2>n1 – целые числа;  - так называемые, волновые числа линий – величины, обратные длине волны соответствующих колебаний:
- так называемые, волновые числа линий – величины, обратные длине волны соответствующих колебаний:
Е = h·ν = h· C/λ, соответственно λ = C/ν, тогда  = 1/λ= ν/С.
= 1/λ= ν/С.
Еще раз отметим, что модель атома, предложенная Резерфордом, не объяснила накопленных данных по спектральным свойствам атомов, более того, она фактически им противоречила. Это все прекрасно понимал и сам Э.Резерфорд. Он откровенно признавал, что для устранения и построения полноценной теории строения атома на тот момент не было достаточной информации о свойствах микрочастиц (в частности, электронов). Поэтому важнейшим ценным результатом считал обоснование наличия в составе атома тяжелой положительной частицы и называл предложенную модель "ядерной".
Наличие ядра в последующих моделях никогда не оспаривалось. Уточнялся их состав, анализировалась природа внутриядерных сил, изучались особенности реакций распада и синтеза ядер. Решающий вклад в эти исследования внес Э.Резерфорд и его ученики. Им был предложен термин "протон" (как название ядра самого простого атома водорода), теоретически обосновано наличие нейтронов в ядрах других атомов, предсказано наличие изотопов и многое другое.
Но самым сложным долгое время оставалось описание законов движения электронов. Законы классической механики И.Ньютона не давали согласия с важнейшими (в первую очередь, оптическими) свойствами атомов. В 1913г. Н.Бор впервые попытался описать энергетические состояния электрона в простейшем атоме водорода с использованием квантовой теории электромагнитного излучения, незадолго до этого разработанной М.Планком. Последовательно обосновать свою модель атома Н.Бору не удалось, поэтому он сформулировал ее основные положения в виде постулатов (неочевидные утверждения, данные без доказательства). Это было явным недостатком модели, но в, то же время, она была внутренне достаточно хорошо согласована. С помощью высказанных идей было дано качественное объяснение устойчивости электронной структуры атома (почему электрон не падает на ядро), линейчатого спектра испускания атомов. расчетным путем удалось получить важные атомные характеристики водорода, прекрасно согласовавшиеся с экспериментом (радиус атома, длины волн тех спектральных линий, которые находятся в видимой и в ближней инфракрасной областях энергетического спектра[1]). Более того, Бор предсказал наличие еще нескольких серий в спектре испускания атома водорода (в ультрафиолетовой и дальней инфракрасной областях). В 1915-1953гг. соответствующий участок спектра атома водорода был экспериментально установлен и расшифрован Лайманом (1915г.), Брэкетом (1922г.), Пфундом (1924г.) и Хемфри (1953г.).
В современной учебной литературе постулаты Н.Бора обычно формулируются следующим образом:
– В атоме водорода электрон вращается вокруг ядра по некоторой стационарной круговой орбите и удерживается на ней под действием центростремительной силы кулоновского взаимодействия.
Стационарность орбит подразумевала неизменность их характеристик, в том числе и энергии. Таким образом, обосновывалась стабильность атома: электрон на стационарной орбите не должен испускать (терять) энергию. Электростатический характер центростремительной силы позволяет записать выражение:
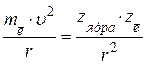 или в системе СИ
или в системе СИ  , (1.3)
, (1.3)
где mē, zē, υ – масса, заряд электрона и скорость его движения по орбите радиусом r вокруг ядра с зарядом zядра, ε0 – относительная диэлектрическая проницаемость вакуума.
– В атоме имеется множество разрешенных стационарных орбит, энергия которых меняется дискретно (квантуется).
Строго говоря, Н.Бор постулировал представление о квантованности момента количества движения электрона на разных орбитах:
 или mē·υ·r = n·ћ, (1.4)
или mē·υ·r = n·ћ, (1.4)
Здесь произведение в левой части равенства – момент количества движения электрона по орбите радиусом r, h – постоянная Планка, ћ = h/2·π– часто называют постоянной Дирака, n – целочисленный сомножитель (квантовое число, n ≥ 1). Таким образом, момент количества движения электрона в атоме по модели Бора не может иметь любые (произвольные) значения, а зависит от выбранного значения n:
| Некоторые возможные значения n | |||
| Соответствующие значения момента количества движения электрона | ћ | 2·ћ | 3·ћ |
Как будет показано ниже, это привело к выводу о дискретности энергетических состояний электрона. Состояние атома, когда электрон находится на орбите с минимальной энергией, называется основным, а все прочие – возбужденными. Таким образом, энергия электрона может меняться только при переходе с одной стационарной орбиты на другую (квантовый скачок). Для возбуждения электрона (атома) требуется поглощение энергии (обычно тепловой, но возможны и другие варианты), а при переходе на орбиты с более низкой энергией должно наблюдаться выделение энергии. Причем количество однократно выделяемой порции энергии (квант) равно разности энергий соответствующих орбит:
Екванта энергии = h·ν = Еорбиты na– Еорбиты nb (1.5)
(na> nb)
Из этого выражения следует, что величина кванта энергии (длина волны порции излучения) зависит от номеров орбит. Это качественно объясняет линейчатость спектра испускания атомов.
Таким образом, с помощью сформулированных постулатов Н.Бору удалось преодолеть принципиальные недостатки планетарной (ядерной) модели строения атома, предложенной Э.Резерфордом.
Теперь рассмотрим подробней предложенные количественные соотношения:
 (1.6)
(1.6)
mē·υ·r = n·ћ. (1.7)
В этой системе уравнений две величины были на тот момент неизвестны: скорость движения электрона и радиус орбиты. Они обе могут быть выражены через константы, входящие в эти выражения.
Если обе части первого уравнения умножить на mē·r3, получим
 (1.8)
(1.8)
Левая часть этого равенства представляет собой квадрат левой части выражения (1.4), тогда и правая часть равенства (1.8) может быть приравнена квадрату правой части выражения (1.4):
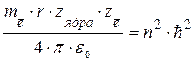 (1.9)
(1.9)
Отсюда 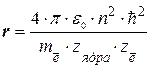 или
или 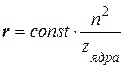 (1.10)
(1.10)
Если данное выражение подставить в уравнение (1.4), то получим
 (1.11)
(1.11)
Видно, что радиусы орбит и скорости движения электрона по ним меняются дискретно в зависимости от значения квантового числа n:с увеличением номера орбиты растет ее размер и уменьшается скорость электрона на ней. Используя значения соответствующих констант, можно, например, рассчитать радиус первой боровской орбиты (радиус атома водорода в основном состоянии):
rn=1= 0.53 Ǻ
(предварительные оценки, основанные на свойствах жидкого
и твердого водорода, давали результат ~1Å).
Энергетический спектр водорода можно проанализировать, если получить формулу для полной энергии электрона в зависимости от главного квантового числа:
Кинетическая энергия движения электрона
Екин = mē·υ2/2 или после подстановки υ из формулы (1.11)
Екин = 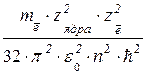 или Екин =
или Екин = 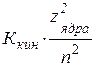 (1.12)
(1.12)
Дата добавления: 2014-11-13; просмотров: 351; Мы поможем в написании вашей работы!; Нарушение авторских прав |