
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Правила квантования
Прежде, чем обсуждать смысл волновых функций и их зависимость от координат, разберемся в целочисленных параметрах. Напомню, что в модели Н.Бора постулировалась квантованность момента количества движения (через квантовое число n). В модернизированной теории Бора-Зоммерфельда использовались уже три квантовых числа. Но они вводились лишь из необходимости улучшить модель, чтобы иметь возможность объяснить вновь открываемые факты о тонкой структуре спектров.
В современной модели строения атома квантовые числа не навязываются, не вводятся искусственно, а появляются в ходе решения волнового уравнения движения электронов. Напомню, что решением волнового уравнения для движущегося в атоме электрона является волновая функция электрона, которая, в свою очередь, зависит от многих переменных. Ее точное решение возможно только для атома водорода и других водородоподобных частиц (He+, Li2+и т.п.). Решение находится проще, если координаты точек задавать не в декартовой (прямоугольной) системе, а в сферической.
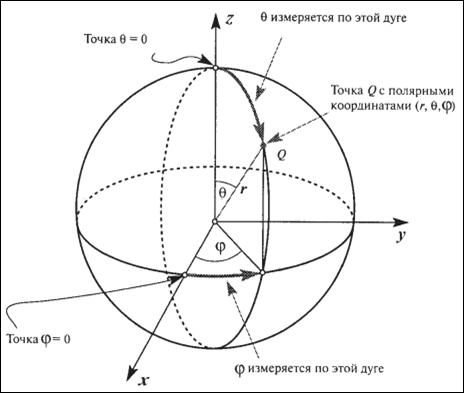
| Рисунок 1.7 – Определение полярных координат (r,θ,φ) для точки Q; r – радиальная координата, θ и φ – угловые координаты. Показаны также оси прямоугольной системы координат (x,y,z). В центре рисунка находится точка отсчета, соответствующая началу координат. |
В этом случае координаты точки задаются одним линейным параметром (радиус-вектором r, характеризующим расстояние от начала координат до рассматриваемой точки) и двумя угловыми (θ и φ). Основываясь на простых тригонометрических соотношениях, можно показать, что координаты в сферической и прямоугольной системах связаны соотношениями:
x = r·sinθ·cosφ, y = r·sinθ·sinφ, z = r·cosθ. (1.25)
В полярных координатах решение облегчается, т.к. удается выполнить процедуру разделения переменных и представить волновую функцию, как произведение трех других, каждая из которых зависит от меньшего числа параметров:
Ψ = f (x,y,z; n,m,l) = R(r;n,l)·Θ(θ;l,m)·Φ(φ;m). (1.26)
В полученном выражении R(r;n,l) называют радиальной составляющей волновой функции Ψ(зависит от главного и орбитального квантовых чисел, а также радиус-вектора). Два последующих сомножителя – угловые составляющие волновой функции.
Для атома водорода угловые составляющие являются константами, поэтому рис.1.6 по сути, является графиком квадрата радиальной составляющей (точнее R2·dV).
Причем, анализом соответствующих уравнений может быть показано, что квантованными (дискретно меняющимися) оказываются не только энергия электрона, но и орбитальные радиусы, а также форма и расположение в пространстве электронных облаков. Наша задача состоит в том, чтобы, не вникая подробно в методы решения волнового уравнения, а также, получаемых из него волновых функций, познакомиться с некоторыми частными итоговыми формулами и усвоить какие квантовые числа в них встречаются, как и на какие свойства электронных облаков, они влияют. Но вначале необходимо усвоить правила квантования, взаимосвязь между разрешенными (квантово-механической теорией) значениями квантовых чисел.
– Главное квантовое число n может принимать любые положительные целочисленные значения:
n = 1; 2; 3; 4; ...∞.
Главное квантовое число входит в формулы, по которым могут быть рассчитаны энергия электрона и орбитальные радиусы в одноэлектронных частицах. Они полностью совпадают с полученными ранее в рамках теории Н.Бора (1.10, 1.15 на стр. 14, 15). Для того, чтобы упростить подобные выражения, их обычно приводят не в системе СИ, а в атомных единицах:
Eорб. =  , rорб =
, rорб =  . (1.27)
. (1.27)
Здесь Ео – энергия электрона в атоме водорода на атомной орбитали с n =1 (в основном состоянии), rо – орбитальный радиус атома водорода в основном состоянии. Причем, как видно из формулы (1.15), Ео < 0. Поэтому с ростом заряда ядра энергия становится все более отрицательной (уменьшается), а при увеличении n – менее отрицательной (растет). Соответственно, состояния электрона с разными значениями n называют энергетическими уровнями. Говорят: главное квантовое число n определяет уровень энергии электрона и размер создаваемого им электронного облака. Минимальной энергией обладает электрон на первом энергетическом уровне. При устремлении n к бесконечности энергия взаимодействия с ядром стремится к нулю, что равносильно полной потере электрона. Анализируя формулу для орбитального радиуса нетрудно сделать вывод, что при увеличении n растет размер электронного облака.
– Орбитальное квантовое число l может принимать целочисленные значения от нуля до (n-1):
l = 0; 1; 2; 3;…(n-1).
Орбитальное квантовое число (наряду с n) влияет на энергию электрона и размер электронных облаков в многоэлектронных атомах. В аналитическом (формульном) виде зависимость энергии от n и l не может быть представлена, т.к. для многоэлектронных частиц уравнение А.Шредингера не имеет точных решений. Межэлектронные взаимодействия могут быть полуколичественно учтены на основе сопоставления эффектов экранирования и проникновения электронных облаков (кратко будут разобраны позднее). Таким способом удается показать, что при одинаковых значениях n связь электронов с ядром ослабевает при увеличении l. То есть с ростом орбитального квантового числа растет и энергия электрона. Поэтому состояния электрона с разными значениями l называют энергетическими подуровнями. Причем для их обозначения обычно используют не численные значения l, а буквенные символы:
Таблица 1.1
Численные значения, обозначения орбитального квантового числа,
форма электронных облаков
| Численное значение орбитального квантового числа l | 4… | ||||
| Буквенное обозначение энергетического подуровня | s | p | d | f | g… |
| Форма электронного облака | сфера | объемная восьмерка (гантель) | две скрещенные гантели (четыре лепестка) | три скрещенные гантели (шесть лепестков) | четыре скрещенные гантели (восемь лепестков)... |
Кроме того, поскольку орбитальное квантовое число входит в угловую составляющую волновой функции (см. (1.26)), оно влияет на форму электронных облаков (см. таблицу 1.1).
Рассмотрим взаимную связь главного и орбитального квантовых чисел. Из правил квантования для l следует, что его минимальное разрешенное значение равно нулю, а максимально возможное ограничено выбранным значением главного квантового числа. Например, при n = 1 орбитальное число может иметь только единственно возможное значение l = 0. Таким образом, в первом энергетическом уровне теорией разрешен только s-подуровень. При n = 2 орбитальное квантовое число может иметь уже два значения: минимальное l = 0 и максимальное l = 1. Поэтому во втором энергетическом уровне имеется два подуровня: s и р. Аналогичным образом можно показать, что в каждом следующем энергетическом уровне будут разрешены дополнительные подуровни: d, f и так далее (в порядке латинского алфавита):
Таблица 1.2
Связь между разрешенными значениями
главного и орбитального квантовыми числами
| Численное значение главного квантового числа n (номер энергетического уровня) | ||||
| Разрешенный набор подуровней | s | s, p | s, p, d | s, p, d, f |
| Обозначения подуровней | 1s | 2s, 2p | 3s, 3p, 3d | 4s, 4p, 4d, 4f |
– Магнитное квантовое число m может принимать целочисленные значения в интервале от –l до +l, включая ноль:
m = –l … 0 … +l.
Магнитное квантовое число входит в угловую составляющую волновой функции и влияет на расположение (ориентацию) электронного облака в пространстве. Поскольку каждое электронное облако представляет собой атомную орбиталь, то число разрешенных значений m соответствует числу возможных ориентаций электронных облаков (числу разрешенных АО).
С учетом вышесказанного можно предложить еще одно определение для атомной орбитали. Это не только "пространство, заполненное движущимся" (электронное облако), но и "квантовая возможность" двигаться в поле данного ядра по конкретному волновому закону, определяющемуся сочетанием квантовых чисел n, l и m (эти квантовые числа полностью определяют волновую функцию электрона). Такая "квантовая возможность" подразумевает, в том числе, и такое понятие как "пустая атомная орбиталь".
Из правил квантования следует, что возможные значения m ограничены выбранным значением l, спектр которых, в свою очередь, определяются выбором главного квантового числа n.
Таблица 1.3
Взаимосвязь между тремя квантовыми числами
| Главное квантовое число (энергетичес-кий уровень) | Разрешенные значения l (энергетические подуровни) | Разрешенные значения m | Число атомных орбиталей (АО) | Обозначения (названия) АО |
| n = 1 | l = 0 (1s – подуровень) | одна | 1s | |
| n = 2 | l = 0 (2s – подуровень) l = 1 (2p – подуровень) | –1; 0; +1 | одна три | 2s 2рx;2py;2pz |
| n = 3 | l = 0 (3s – подуровень) l = 0 (3p – подуровень) l = 0 (3d – подуровень) | –1; 0; +1 –2; –1; 0; +1; +2 | одна три пять | 3s 3рx; 3py; 3pz 3dxy; 3dxz; 3dyz; 3dx2–y2; 3dz2 |
| n = 4 | l = 0 (4s – подуровень) l = 0 (4p – подуровень) l = 0 (4d – подуровень) l = 0 (4f – подуровень) | –1; 0; +1 –2; –1; 0; +1; +2 –3;–2;–1;0;1;2;3 | одна три пять семь | 4s 4рx; 4py; 4pz 4dxy и т.п. 4fxyz и т.п. |
Из результатов, приведенных в таблице, видно, что на s–подуровнях первого, второго и последующих уровней имеется только по одной атомной орбитали (т.к. для орбиталей s–подуровня возможно только одно значение магнитного квантового числа). Они отличаются друг от друга размерами (и числом максимумов на графиках радиального распределения электронной плотности (рис.1.6, 1.8)).

| Рис. 1.8 – Графики радиальных составляющих волновой функции для водородоподобных орбиталей первого, второго и третьего энергетических уровней. |
Из рис.1.8 следует, что, 2р-орбиталь характеризуется меньшим орбитальным радиусом, чем 2s-орбиталь. Однако на графике для радиального распределения 2s-облака имеется дополнительный внутренний максимум. Это говорит о том, что 2s-электрон довольно часто бывает вблизи ядра и за счет такого проникновения в область 1s-облака усиливает свое притяжение к ядру, 2s-орбиталь становится энергетически более выгодной. В третьем энергетическом уровне максимальный эффект проникновения, опять же, демонстрируют электроны 3s-орбитали. Хуже всего ядро атома будет удерживать электроны на непроникающих 3d-орбиталях – эти орбитали лучше заэкранированы от ядра внутренними электронными облаками и будут иметь самую высокую энергию в третьем энергетическом уровне. Более того, как будет показано при обсуждении правил В.Клечковского, 3d-орбитали оказываются более высоколежащими, чем даже 4s-орбиталь, которая за счет внутренних максимумов обеспечивает более сильное взаимодействие с ядром атома (иными словами, эффективный заряд ядра, действующий на 4s-электроны, оказывается выше, чем для 3d-электронов).
На р–подуровнях разрешены три АО: три значения m разрешают три разных ориентации р–электронных облаков в пространстве вокруг ядра. Как видно из их названий, они располагаются своими лепестками вдоль прямоугольных осей координат (рис.1.9).
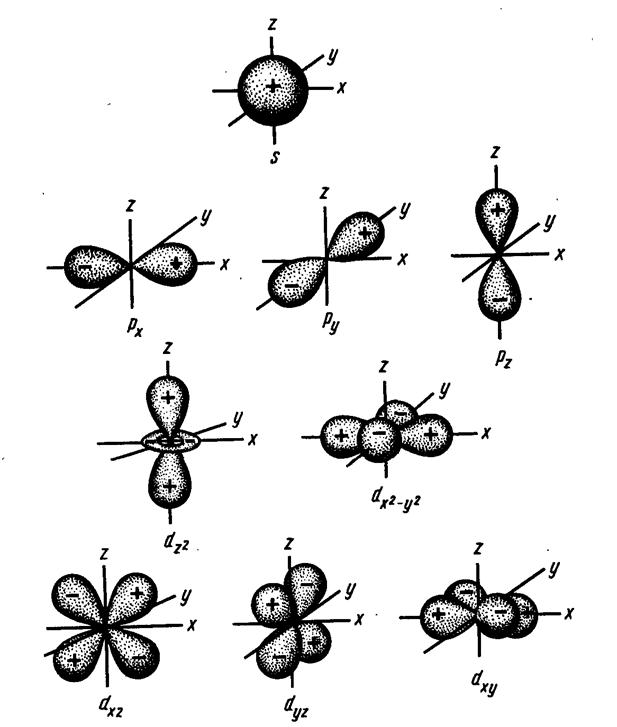
| Рис. 1.9 – Графики для квадратов угловых составляющих волновых функций, передающих форму и взаимное расположение в пространстве s-, p- и d- водородоподобных орбиталей (показаны знаки волновых функций). |
На d–подуровнях разрешены пять АО. У них более сложная форма, поэтому в названиях d–орбиталей обычно приходится указывать две координатных оси, лежащих в одной плоскости с лепестками орбиталей. Орбитали ndxy ndx2–y2 лежат в плоскости x0y, но повернуты друг относительно друга на 45° (лепестки орбиталей ndx2–y2 располагаются вдоль осей координат, а лепестки орбиталей ndxy – по биссектрисам координатных углов). Так же, как и в случае s–орбиталей, с увеличением n растут размеры облаков, меняется число максимумов на графиках R2·4πr2. Напомню, что орбитальный радиус находится как расстояние от ядра до самого дальнего максимума (самого дальнего "сгустка" электронного облака).
Таким образом, сочетание разрешенных значений трех квантовых чисел (n, l, m) полностью определяют все свойства атомных орбиталей (электронных облаков). После подстановки в соответствующие формулы они формируют закон движения электрона в поле ядра и других электронов (Ψ). Однако, изучение спектральных и ряда других свойств атомов в магнитном поле привело к выводу, что электроны обладают еще одним "собственным", "внутренним" свойством, не зависящим от влияния других частиц. Это свойство имеет два неизменных значения (квантуется). Поначалу был высказано предположение, что этим свойством является способность электрона вращаться, как волчок вокруг собственной оси. Для описания такого поведения было введено спиновое квантовое число (спин – "веретено")–s(или mS): +½ и -½. Позднее было показано, что для количественного описания эффектов взаимодействия электрона с магнитным полем требовалась бы скорость вращения, превышающая скорость света. Строгое обоснование этому свойству электрона может быть дано на основе теории относительности, но представление о вращении электрона по-прежнему используется как удобный, наглядный образ.
Итак, для полного описания всех известных на настоящий момент свойств электрона, для описания электронного строения атомов необходимо использовать четыреквантовых числа:n, l, m, s.
Дата добавления: 2014-11-13; просмотров: 670; Мы поможем в написании вашей работы!; Нарушение авторских прав |