Полная энергия электрона в атоме водорода

Е_Σ = – 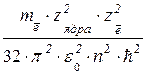или Е_Σ = – .(1.15)

Тогда при переходе с высоколежащей на низколежащую орбиту выделяется квант энергии

h·ν = ·(1/n_a² – 1/n_b²) (1.16)

Соответственно, частота колебаний испускаемого электромагнитного излучения находится:

ν = ·(1/n_a² – 1/n_b²) (1.17)

Обычно для характеристики спектральных свойств атомов (и веществ) используют волновые числа (стр.10), то:

(1.18)

и, объединяя уравнения (1.16) и (1.18), получаем:

= R·(1/n_a² – 1/n_b²) (1.19)

где R – константа Ридберга, ранее найденная опытным путем при изучении атомных спектров и впервые рассчитанная Н.Бором через фундаментальные константы:

R = (1.20)

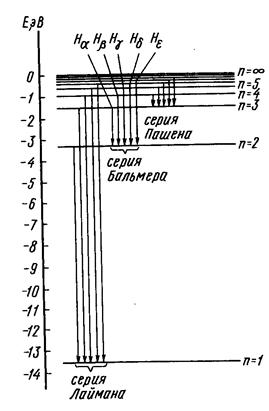
Рисунок 1.4 – Схема энергетических уровней в атоме водорода (модель Бора) и квантовые переходы, складывающиеся в спектральные серии (без учета тонких эффектов).

С использованием этой формулы, как уже отмечалось ранее (стр.11), Н.Бору удалось обосновать известные на тот момент спектральные серии Бальмера и Пашена, как результат выделения энергии при возвращении возбужденных электронов на вторую и третью атомные орбиты. Кроме того, была предсказана серия линий, которые должны были соответствовать переходу возбужденных электронов в основное состояние атома водорода (на орбиту с n=1,… серия Лаймана,… см. стр.11, а также рис.1.4).

Теория Н.Бора, разработанная для атома водорода, позволила успешно объяснить спектральные свойства, энергии ионизации и других одноэлектронных частиц (He⁺, Li²⁺, В³⁺и т.п.). Однако попытки применить эту модель для описания спектров сложных атомов (даже в случае двухэлектронного атома Не) оказались неудачными. К тому же, в ходе совершенствования техники эксперимента было показано, что даже спектр одноэлектронных частиц состоит не из набора отдельных линий. В зависимости от разрешающей способности спектрометра или отдельные линии (тонкая структура), или все (сверхтонкая структура спектров) "расщеплялись" на сочетания нескольких близко расположенных дублетов, триплетов и более сложных мультиплетов.

В 1916-1924гг. А.Зоммерфельд опубликовал несколько работ, в которых, модернизируя идеи Бора (теория Бора-Зоммерфельда), показал, что тонкую структуру спектров атома водорода, Не⁺, щелочных металлов можно объяснить, если допустить, что в пределах одного энергетического уровня (при одном значении n) имеется несколько близких по энергии орбит: не только круговых, но и эллиптических. Он ввел понятие второго (побочного) квантового числа (k), связанного с орбитальным движением электронов. При этом предполагалось, что главное квантовое число (n) определяет размер большой полуоси данного семейства эллипсов (в частном случае окружности – ее радиус). Величина малой полуоси определяется побочным квантовым числом, которое также принимает только целочисленные значения, но не больше главного. Например, для главного квантового числа n = 3 возможны три типа эллипсов (3₁, 3₂ и 3₃), для которых соотношение между величинами большой и малой полуоси равны 3:1, 3:2 и 3:3, соответственно. В последнем случае имеем дело с частным случаем эллипса – окружностью. Это позволило объяснить небольшое различие в энергии орбит с одинаковым главным квантовым числом n.

Если электроны вращаются только по круговым орбитам, то электрон, находящийся на внешней орбите, слабей связан с ядром не только из-за большего расстояния, но и по причине экранирования заряда ядра внутренними электронами: в идеале каждый внутренний электрон формально на единицу уменьшает величину заряда, действующего на последующие электроны. В модернизированной модели Бора-Зоммерфельда (рис.1.5) при одном и том же n электрон на более вытянутой орбите в процессе своего движения оказывается непосредственно вблизи ядра и, тем самым, проникает под экранирующую оболочку и поэтому на части своей траектории испытывает действие возрастающего заряда ядра. Отсюда следует, что сильно вытянутые эллиптические орбиты будут обладать дополнительной стабильностью, более низкой энергией.

Однако даже такого усовершенствования оказалось недостаточно, чтобы объяснить сверхтонкую структуру спектров (пришлось вводить, уже малообоснованно, понятие о третьем квантовом числе). Еще большие проблемы возникали при попытке объяснить структуру периодической системы элементов. Такие попытки предпринимались, но они, опять же, требовали введения дополнительных правил, ограничений, не вытекавших из теории. И, наконец, теории Бора, Бора-Зоммерфельда были совершенно непригодны для количественного описания межатомного взаимодействия, теории химической связи. Например, не удалось получить приемлемого совпадения с экспериментальными значениями энергии связи, межатомного расстояния не только в простейшей молекуле Н₂, но и в одноэлектронной частице Н₂⁺. расчет по модели Н.Бора давал отрицательное значение энергии связи для молекулярного иона Н₂⁺. Это означало, что существовать он не может. На самом деле ион такой известен и энергия связи в нем составляет ~255 кДж/моль.