
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Свойства операций над событиями
1. 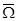 =Ø 6. А
=Ø 6. А 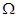 = А
= А
2. А + А = А 7. А Ø = Ø Коротко. Если А 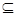 В, то
В, то
3. А А = А 8 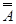 = АА + В = В
= АА + В = В
4. А + 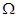 =
= 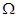 9.
9. 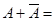
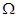 А В = А
А В = А
5. А + Ø = А 10. 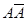 = Ø
= Ø
Коммутативность операций
А + В = В + А; А В = В А
Ассоциативность операций
А + (В + С)=(А + В) + С = А + В + С А(В С) = (А В) С = А В С
Дистрибутивность операции сложения относительно умножения
А (В + С) = А В + А С
Дистрибутивность операции умножения относительно сложения
А + (В С) = (А + В)(А + С)
Пример. Вычислим (A+B)(A+C)=AA+BA+AC+BC=A+BC.
В самом деле, BAÌA, ACÌA, AA=A, тогда AA+BA=A, A+AC=A.
Правило двойственности (теорема де Моргана)
Для всякого сложного события, выраженного через сумму и произведение (даже счетного количества) событий, противоположное событие может быть получено путем замены событий им противоположными и замены знака произведения на знак суммы, а знака суммы на знак произведения, при оставлении порядка операций неизменным
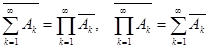
Пример. 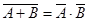
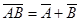
Дата добавления: 2014-12-30; просмотров: 403; Мы поможем в написании вашей работы!; Нарушение авторских прав |