
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Геометрическая вероятность
Формула классической вероятности применяется только в схеме случаев, что встречается довольно редко. Отношение Р(А)= NA/N представляет собой «долю» благоприятных исходов среди всех возможных исходов. Аналогичным образом подсчитывают вероятность события в некоторых более сложных случаях, когда имеется бесконечное число равновозможных исходов.
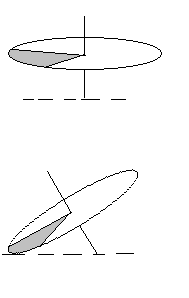
| Событие А – волчок касается плоскости точкой из окрашенного сектора.
Множество точек на ободе в окрашенном секторе имеет мощность континуума. Делим всю окружность на N маленьких одинаковых дуг. Число дуг на окружности, принадлежащих окрашенному сектору, пусть равно NA.
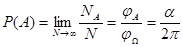 .
В общем случае имеется мера mes .
В общем случае имеется мера mes  соответствующая соответствующая  (в нашем случае mes (в нашем случае mes 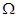 = 2 = 2  ) и мера mes А, соответствующая А (в нашем случае mesА = ) и мера mes А, соответствующая А (в нашем случае mesА =  ) )
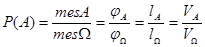 и т.д. и т.д.
|
Пример. Задача о встрече. Два студента договорились встретиться от 10 до 11 часов на определенном месте, причем первый пришедший на место ждет товарища 15 минут и уходит. Какова вероятность встречи?
Выберем начало системы координат в точке (10, 10). Отложим по осям системы координат x- время прихода первого студента, y – время прихода второго студента.
 Тогда множество |x-y|<1/4, 0<x<1, 0<x<1, 0<y<1
Тогда множество |x-y|<1/4, 0<x<1, 0<x<1, 0<y<1
содержит точки (события) встречи студентов. Его мера (площадь) mesA равна 1- (3/4)2 = 7/16. Так как mesW =1, то P(A) = 7/16.
Статистическая вероятность
Формулы классической вероятности и геометрической вероятности справедливы только для случая равновозможных исходов. В действительности мы на практике имеем место с неравновозможными исходами. В этих случаях можно определить вероятность случайного события, используя понятие частоты события. Допустим, что нам требуется определить вероятность того, что в испытании произойдет событие А. Для этого в одинаковых условиях проводятся испытания, в каждом из которых возможны два исхода: А и 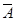 . Частотой события А будем называть отношение числа NA испытаний, в которых зафиксировано событие А к общему числу N испытаний.
. Частотой события А будем называть отношение числа NA испытаний, в которых зафиксировано событие А к общему числу N испытаний.
Вероятностью события А называется предел частоты события А при неограниченном увеличении числа испытаний n 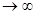 , т.е.
, т.е. 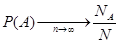 . Так определяется статистическая вероятность события.
. Так определяется статистическая вероятность события.
Заметим, что по классическому, геометрическому и статистическому определениям для вероятности события P(A) выполнены три основных свойства:
P(A)³0, 2) P(W)=1, 3) P(A1+ …+An) = P(A1) + …+P(An), если A1, An попарно несовместны. Однако в этих определениях элементарные события предполагаются равновозможными.
А.Н. Колмогоров отказался от предположения равновозможности элементарных событий, ввел сигма-алгебру событий и распространил третье свойство на счетное число событий. Это дало возможность дать аксиоматическое определение вероятности события.
Аксиоматическое определение вероятности(по А.Н.Колмогорову).
Вероятностью P(A) называется числовая функция, заданная на сигма – алгебре событий, удовлетворяющая трем аксиомам:
1) не отрицательность P(A)³0, "AÎB - сигма – алгебре событий на W
2) нормировка P(W) = 1
3) расширенная аксиома сложения: для любых попарно несовместных событий A1, … An … выполнено
P(A1+ …+An+ …) = P(A1) + …+P(An) +…
(счетная аддитивность).
Итак, по А.Н. Колмогорову вероятность (вероятностная мера) это числовая неотрицательная нормированная счетно - аддитивная функция (множества – события), заданная на сигма – алгебре событий.
Если W состоит из конечного или счетного числа событий, то в качестве сигма – алгебры B может рассматриваться алгебра S событий. Тогда по аксиоме 3 вероятность любого события A равна сумме вероятностей элементарных событий, составляющих A.
Вероятностным пространствомназывается тройка (W, B, P).
Дата добавления: 2014-12-30; просмотров: 332; Мы поможем в написании вашей работы!; Нарушение авторских прав |