Формула вероятности суммы совместных событий

(теорема сложения вероятностей)

В соответствии со свойством 3) классической вероятности вероятность суммы несовместных событий равна сумме вероятностей этих событий. А если события совместны?

Пусть мы имеем два совместных события А и В. Преобразуем их сумму в сумму несовместных событий (см. диаграмму Венна).

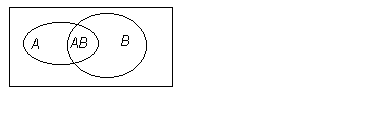
Подставляя второе выражение в первое, получим

. (2.10)

Пример. По мишени один раз стреляют два стрелка. Вероятность попадания первого стрелка в мишень р₁ = 0,7, второго – р₂ = 0,8. Какова вероятность того, что кто-нибудь из них попадет в мишень?

А = А₁ + А₂, где А попадание в мишень;

А₁ – попал первый стрелок;

А₂ – попал второй стрелок.

Р(А) = Р(А₁ + А₂) = Р(А₁) + Р(А₂) – Р(А₁А₂)=

= Р(А₁) + Р(А₂) – Р(А₁ )Р(А₂)=

= 0.7 + 0,8 – 0,7· 0,8 = 0,94.

Получим вероятность суммы трех совместных событий.

Получена формула

Р(А + В + С) = Р(А) + Р(В) + Р(С) – Р(АВ) – Р(АС) – Р(ВС) + Р(АВС) (2.11)

Обобщая полученный результат на сумму n совместных событий, получим формулу

(2.12)