Свойства функции распределения. 1) по аксиомам вероятности,

1) по аксиомам вероятности,

2) 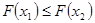, если , т.е. функция распределения – неубывающая функция.В самом деле, 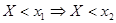, следовательно, .

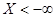3) В самом деле, событие - невозможное, и его вероятность нулевая. Событие 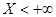- достоверное, и его вероятность равна 1.

4) . Так как события несовместны и событие 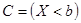есть сумма этих событий, то .

График функции распределения имеет, примерно, следующий вид

F(x)

1

x

Функцию распределения можно определить и для дискретной случайной величины. Ее график будет графиком ступенчатой функции со скачками в p_i в точках x_i , непрерывной слева в этих точках.

F(x)

1

p₃

p₂

p₁

x

x₁ x₂ x₃ x_n

Для непрерывной случайной величины вводится плотность распределения вероятностей.

Плотностью распределения(вероятностей) называется производная функции распределения .

Ясно, что .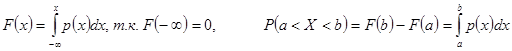

Часто функцию распределения называют интегральным законом распределения, а плотность распределения – дифференциальным законом распределения. Так как 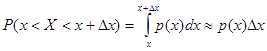, то p(x)dx называется элементом вероятности.

Дата добавления: 2014-12-30; просмотров: 13; Нарушение авторских прав