Условная вероятность.

Часто приходится вычислять вероятность события А при дополнительном условии, что произошло событие В. Такую вероятность будем называть условной и обозначать Р(А/В) (вероятность события А при условии, что событие В наступило).

Если никаких дополнительных условий не накладывается, то вероятность называется безусловной. Это – обычная, определенная выше вероятность.

Рассмотрим пример. Пусть в данной аудитории присутствует N студентов. Среди них N_A –любящих математику, N_B – любящих физику, N_АВ – любящих и математику, и физику. Лектор случайно выбирает одного студента. Введем следующие события:

А – случайно выбранный студент любит математику, В – физику, АВ – и математику, и физику. На диаграммах Венна это выглядит так.

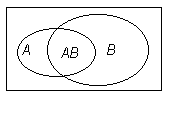Тогда вероятности этих событий равны:

(2.1)

(2.2)

(2.3)

Это безусловные вероятности.

Предположим теперь, что мы захотели узнать вероятность того, что случайно выбранный любитель физики любит еще и математику. В этом случае количество всех возможных исходов N_B (выбираем только любителей физики), а количество благоприятных исходов – N_АВ.

На диаграмме Венна это выглядит так

Тогда, учитывая (2.2) и (2.3), получим

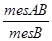= = (2.4)

Мы рассмотрели частный случай. Введем в общем случае следующее формальное определение.

Определение. Пусть В – событие, имеющее ненулевую вероятность, а А произвольное событие.

Положим . (2.5)

Определенную таким образом величину Р(А/В) будем называть условной вероятностью события А при условии В.