Алгебра событий.

Пусть W - пространство элементарных событий. Алгеброй событий S называется такая система случайных событий S, что

1) SÉW, 2) " A, B Ì S Þ A+BÌS, ABÌS, A\BÌS.

Следствие Æ= W\W Ì S

Пусть W содержит конечное число элементов, W= {w₁,…w_n}. Тогда алгебру S можно построить как множество всех подмножеств W.

S={Æ, {w₁}, … {w_n}, {w₁,w₂}, …{w₁,w_n}, …{w_n-1,w_n}, …{w_{1, …,}w_n}}, в ней всего 2ⁿ элементов

Аналогично стоится алгебра для счетного числа событий.

Если в результате опыта стало известно, произошли или нет события A, B, то можно заключить, произошли или нет события , A+B, AB, A\B, поэтому события должны выбираться из определенного класса – алгебры событий.

Для бесконечного (не счетного) числа событий класс событий должен быть сужен. Вводится s- алгебра событий.

Сигма-алгеброй (s-алгеброй) событий Bназывается непустая система подмножеств пространства элементарных событий, такая что

1) AÌBÞ 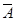ÞB,

2) A₁, A₂, …A_n, …ÌBÞ( A₁+A₂+ …+A_n+, …)ÌB, …ÌB.

Любая сигма-алгебра событий является алгеброй событий, но не наоборот.