
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теорема умножения вероятностей). Независимые события
Из формулы условной вероятности найдем вероятность события АВ и воспользуемся возможностью поменять А и В местами из-за коммутативности произведения событий. Из (2.5) получим
Р(АВ) = Р(В)·Р(А/В) = Р(А)·Р(В/А). (2.6)
Вероятность совместного наступления двух событий (вероятность произведения этих событий) равна произведению вероятности одного из них на условную вероятность другого при условии, что первое событие произошло.
Теорема умножения вероятностей может быть обобщена на случай произвольного числа событий.
Вероятность произведения нескольких событий равна произведению вероятностей этих событий, причем вероятность каждого следующего по порядку события вычисляется при условии, что все предыдущие имели место.
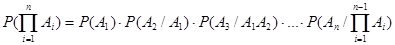 (2.7)
(2.7)
Событие А будем называть независимым от события В, если
P(A/B) = P(A), (2.8)
т.е. если условная вероятность равна безусловной вероятности.
Два события называются независимыми, если наступление одного из них не изменяет вероятность другого. В противном случае события называются зависимыми.
События А1, А2,…, Аn называются независимыми в совокупности, если вероятность их произведения равна произведению их вероятностей
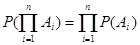 . (2.9)
. (2.9)
Можно показать, что из попарной независимости не вытекает независимость в совокупности
Пример 1. Наугад вытаскивается одна карта из тщательно перетасованной колоды в 36 карт.
А – вытащенная карта – дама;
 4/36 = 1/9;
4/36 = 1/9;
1) Дополнительная информация: произошло событие В – вытащена карта бубновой масти, 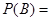 1/4,
1/4, 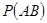 =1/36.
=1/36.

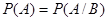
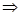 А и В – независимы.
А и В – независимы.
2) Дополнительная информация: произошло событие С – вытащена «картинка» (валеты, дамы, короли),  =12/36,
=12/36, 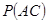 =4/36.
=4/36.

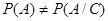
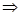 А и C – зависимы.
А и C – зависимы.
Пример 2. На плотной бумаге написано слово «стипендия»

| С | Т | И | П | Е | Н | Д | И | Я |
Разрезав надпись на буквы и перемешав их, вытаскиваем наугад шесть букв.
Какова вероятность того, что из вытащенных букв в порядке вытаскивания получится слово «пенсия»?
Р(«пенсия») = Р(п)·Ре/п)·Р(н/пе)·Р(с/пен)·Р(и/пенс)·Р(я/пенси) =
= 1/9· 1/8 · 1/7 · 1/6 · 2/5 · 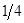 = 1/30240
= 1/30240
Решая эту задачу методами комбинаторики, получим
Р(«пенсия») = 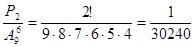 .
.
Дата добавления: 2014-12-30; просмотров: 311; Мы поможем в написании вашей работы!; Нарушение авторских прав |